Page 31 - 《应用声学》2021年第1期

第 40 卷 第 1 期 张经科等： 平面波超声成像中的波束合成方法研究进展 27

图 5(d)) 相比于传统频域波束合成方法重建的图像 内存占用问题，却仍然面临着重建耗时过长的问
(图 5(a) 和图 5(b)) 的对比度有着显著的提升，背景 题。Besson 等 [37] 提出了一种无须存储的在线测量
中的噪声也得到了较好的抑制。Schiffner 等 [32] 提 矩阵构建方法，高效地利用了图形处理器(Graphics
出了一个时间-频率混合模型，来分开处理带宽内的 processing unit, GPU) 的并行特性，同时计算不同
不同频率，提高了模型对于畸变效应的鲁棒性。这 成像网格点上的冲激响应，进一步解决了内存占用
类方法的主要问题在于，其测量矩阵将占用巨大的 的问题，并首次将重建单角度平面波的时间减少至
内存(数百GB)。 200 ms 以下，为实时重建提供了可能。就图像质量
而言，时域逆问题求解方法通常带来分辨率和对比
2.2 时域模型
度的显著提升。图6为Besson等提出的时域模型的
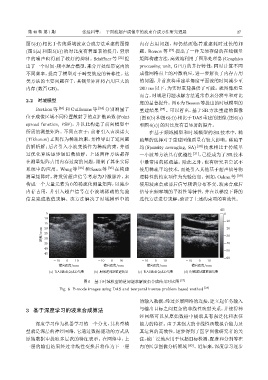
Berthon 等 [33] 和 Guillaume 等 [34] 分别测量了 重建结果 [37] 。可以看出，基于 SR 方法重建的图像
位于成像区域不同位置散射子的点扩散函数(Point (图6(b) 和图 6(d)) 相比于 DAS重建的图像 (图 6(a)
spread function, PSF)，并以此构建了前向模型中 和图6(c))的对比度有着显著的提升。
所需的测量矩阵。不同点在于：前者引入吉洪诺夫 在基于频域模型和时域模型的 SR 技术中，稀
(Tikhonov) 正则作为稀疏约束，并推导出了逆问题 疏基的选择对于重建图像质量有较大影响。稀疏平
的解析解；后者引入小波变换作为稀疏约束，并通 均 (Sparsity averaging, SA) [38] 技术相比于传统单
过优化算法逐步逼近数值解。上述两种方法都存 一小波基方法具有优越性 [31] ，已经成为了 SR 技术
在测量矩阵占用内存过高的问题，限制了其在实际 中最常用的稀疏基。除此之外，也有研究者尝试不
系统中的应用。Wang 等 [35] 和 Szasz 等 [36] 在构建 使用稀疏平均技术，而是引入其他基于超声信号物
测量矩阵时，将发射超声信号考虑为冲激脉冲，来 理特性的约束项作为先验信息。例如，Ozkan 等 [39]
构成一个大量元素为 0 的稀疏化测量矩阵，以减少 使用波束合成前后信号频谱分布不变、波束合成后
内存占用，并引入超声信号在小波域稀疏的先验 信号在频率域的平滑性等特性，并在以梯度下降的
信息完成数值求解。该方法解决了时域模型中的 迭代方法进行求解，验证了上述约束项的有效性。

dB
5 0
10
-10
15 -20
20
ງए/mm 25 -30
30
35 -40
40
-50
45
-60
-10 0 10 -10 0 10 -10 0 10 -10 0 10
ഷՔᡰሏ/mm ഷՔᡰሏ/mm ഷՔᡰሏ/mm ഷՔᡰሏ/mm
(a) DASฉౌՌੇՑፇ౧ (b) ௑۫ᤤ᫈ᮥ᧘थፇ౧ (c) DASฉౌՌੇՑፇ౧ (d) ௑۫ᤤ᫈ᮥ᧘थፇ౧
图 6 基于时域模型的逆问题求解波束合成结果对比图 [37]

Fig. 6 B-mode images using DAS and temporal inverse problem based method [37]

的输入数据，经过多层网络的连接，建立起任务输入
3 基于深度学习的波束合成算法 与输出目标之间复杂的非线性映射关系，并使得神
经网络可以从原始数据中提取具有强泛化和表征
深度学习作为机器学习的一个分支，其典型模 能力的特征。由于其强大的非线性函数拟合能力及
型就是深层的神经网络，它通过数据驱动的方式从 其运算的高效性，逐步得到了医学图像研究者的关
原始数据中提取多层次的特征表示。在网络中，上 注，被广泛地应用于包括目标检测、配准和分割等在
一层的输出结果经过非线性变换后将作为下一层 内的医学图像分析领域 [40] 。近年来，深度学习逐步