Page 35 - 《应用声学》2021年第2期

第 40 卷 第 2 期 许凡等： 基于三元伪随机序列集的多声源房间脉冲响应测量方法 203

这实际上是一个周期内的采样序列{−1, 1, 1}重复5次：
e((n − 1) mod 15) = {1, 1, −1, 1, 1, −1, 1, 1, −1, 1, 1, −1, 1, 1, −1},

e((n − 2) mod 15) = {1, −1, 1, 1, −1, 1, 1, −1, 1, 1, −1, 1, 1, −1, 1}.

当τ = 3时，e((n − 3) mod 15)与e(n)相同，故不重复的e((n − τ) mod L) 只有3个，这样Kasami序列为
ks 0 (n) = {1, −1, −1, −1, 1, 1, 1, −1, 1, −1, 1, 1, −1, −1, 1},

ks 1 (n) = {1, −1, −1, −1, 1, 1, 1, −1, 1, −1, 1, 1, −1, −1, 1},
ks 2 (n) = {−1, −1, 1, 1, 1, −1, 1, −1, −1, −1, 1, −1, −1, −1, −1},

ks 3 (n) = mls(n) = {−1, −1, −1, 1, 1, 1, 1, −1, 1, −1, 1, 1, −1, −1, 1}.

3.0 600
2.5 400
ᒭᄱТѦ஝/10 5 1.5 ᒭᄱТѦ஝ 200 0
2.0

1.0
0.5 -200
0 -400
-0.5 -600
-0.5 0 0.5 1.0 1.5 2.0 2.5 3.0 100 105 110 115 120 125 130
n/10 5 n
(a) KasamiऀѵᒭᄱТѦ஝ (b) KasamiऀѵᒭᄱТѦ஝ࡍᦊஊܸڏ

3.0 600
2.5 400
̉ᄱТѦ஝/10 5 1.5 ̉ᄱТѦ஝ 200 0
2.0

1.0
0.5 -200
0 -400
-0.5 -600
-0.5 0 0.5 1.0 1.5 2.0 2.5 3.0 100 105 110 115 120 125 130
n/10 5 n
(c) Kasamiऀѵ̉ᄱТѦ஝ (d) Kasamiऀѵ̉ᄱТѦ஝ࡍᦊஊܸڏ

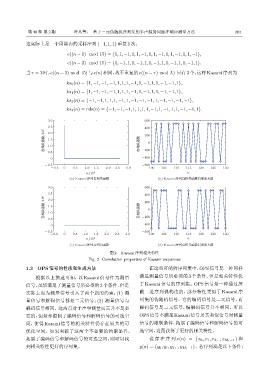
图 2 Kasami 序列相关特性
Fig. 2 Correlation properties of Kasami sequences

1.3 OPS信号的性质和生成方法 在这些可能的序列集中，OPS 信号是一种同样
根据以上描述可知，以 Kasami 信号作为测量 满足测量信号所必须的 3 个条件、但是相关特性优
信号，虽然满足了测量信号所必须的3 个条件，但是 于 Kasami 信号的序列集。OPS 信号是一种通过屏
实际上也为测量信号引入了两个新的约束：(1) 测 蔽二进序列偶构造的，部分特性类似于 Kasami 序
量信号和解码信号都是二元信号；(2) 测量信号与 列集的伪随机信号。它的编码信号是二元信号，而

解码信号相同。这两点对于声学测量而言并不是必 解码信号是三元信号，编解码信号并不相同。所以
要的，但是却限制了编码信号和解码信号的可选空 OPS 信号不满足 Kasami 信号及其类似信号对测量
间，使得 Kasami 信号的相关特性仍存在较大的可 信号的限制条件，拓展了编码信号和解码信号的可
优化空间。如果突破了这两个不必要的约束条件， 选空间，进而获得了更好的相关特性。
拓展了编码信号和解码信号的可选空间，则可以找 设 存 在 序 列 x(n) = {x 0 , x 1 , x 2 , , x M 1 −1 } 和
到相关特性更好的序列集。 y(n) = {y 0 , y 1 , y 2 , , y M 1 −1 }。若序列满足以下条件：