Page 12 - 《应用声学》2021年第4期

496 2021 年 7 月

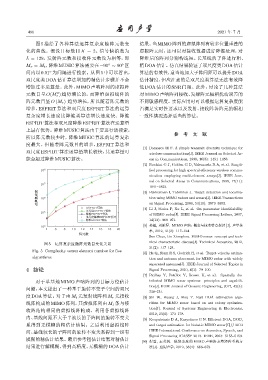
图 5 描绘了各种算法运算复杂度随阵元数变 结果。当MIMO阵列的虚拟阵列有较多位置重叠的
化的曲线。假设目标数目 K = 2、信号快拍数为 虚拟阵元时，还可以对接收数据进行降维处理，对
L = 128，发射阵元数和接收阵元数设为相等，即 降维后的阵列分别构造短、长基线的子阵进行粗、
M r = M t ，降维 MUSIC 算法需要在 −90 ∼ 90 区 精DOA估计。仿真结果验证了双尺度类DOA估计
◦
◦
间内以 0.01 为间隔进行搜索。从图 5 中可以看出， 算法的有效性，适当地加大子阵间距可以提升DOA
◦
双尺度类 DOA 估计算法增加的精估计步骤并不会 估计精度，但应注意的是双尺度类算法无法有效降
增加过多运算量。此外，MIMO 声呐阵列的虚拟阵 低 DOA 估计的 SNR 门限。此外，讨论了几种算法
2
元数目呈 O(M ) 趋势增长的，而降维虚拟线阵的 对MIMO 声呐阵列接收、发射阵元幅相扰动误差的
r
阵元数目呈 O (M r ) 趋势增长，所以随着阵元数的 不同敏感程度。实际应用时可以根据运算复杂度能
增多，ESPRIT 算法和双尺度 ESPRIT 算法的运算 否满足实时性要求以及发射、接收阵各阵元的幅相
复杂度增长速度比降维类算法增长速度快。降维 一致性情况选择适当的算法。
ESPRIT算法和双尺度降维ESPRIT算法在运算量
上最有优势。降维 MUSIC 算法由于要进行谱搜索，
参 考 文 献
所以阵元数较少时，降维 MUSIC 算法的运算复杂
度最大。但随着阵元数目的增多，ESPRIT 算法和
[1] Damasco M F. A simple transmit diversity technique for
双尺度 ESPRIT 算法运算量增长较快，其运算量可 wireless communications[J]. IEEE Journal on Selected Ar-
能会超过降维MUSIC算法。 eas in Communications, 1998, 16(8): 1451–1458.
[2] Foschini G J, Golden G D, Valenzuela R A, et al. Simpli-
10 8 fied processing for high spectral efficiency wireless commu-
nication employing multi-element arrays[J]. IEEE Jour-
nal on Selected Areas in Communications, 1999, 17(11):
10 7
1841–1852.
ᤂካܭాए 10 6 tion using MIMO radars and sonars[J]. IEEE Transactions
[3] Bekkerman I, Tabrikian J. Target detection and localiza-
on Signal Processing, 2006, 54(10): 3873–3883.
ESPRITካข [4] Li J, Stoica P, Xu L, et al. On parameter identifiability
ܳࡇएESPRITካข
10 5
ᬌ፥ESPRITካข of MIMO radar[J]. IEEE Signal Processing Letters, 2007,
ܳࡇएᬌ፥ESPRITካข
ᬌ፥MUSICካข 14(12): 968–971.
10 [5] 孙超, 刘雄厚. MIMO 声纳: 概念与技术特点探讨 [J]. 声学技
4
4 6 8 10 12 14 16 18 20
术, 2012, 31(2): 117–124.
᫼Ћ஝
Sun Chao, Liu Xionghou. MIMO sonar: concept and tech-
图 5 运算复杂度随阵元数目变化关系 nical characteristic discuss[J]. Technical Acoustics, 2012,
31(2): 117–124.
Fig. 5 Complexity versus element number for five
[6] He Q, Blum R S, Godrich H, et al. Target velocity estima-
algorithms tion and antenna placement for MIMO radar with widely
separated antennas[J]. IEEE Journal of Selected Topics in
4 结论 Signal Processing, 2010, 4(1): 79–100.
[7] Pailhas Y, Petillot Y, Brown K, et al. Spatially dis-
对于单基地 MIMO 声呐阵列的目标方位估计 tributed MIMO sonar systems: principles and capabili-
ties[J]. IEEE Journal of Oceanic Engineering, 2017, 42(3):
问题，本文提出了一种基于旋转不变子空间的双尺
738–751.
度 DOA 算法。对于由 M t 元发射线阵和 M r 元接收 [8] Shi W, Huang J, Hou Y. Fast DOA estimation algo-
线阵构成的 MIMO 阵列，其虚拟阵列由 M t 条与接 rithm for MIMO sonar based on ant colony optimiza-
收阵结构相同的虚拟线阵构成。利用各虚拟线阵 tion[J]. Journal of Systems Engineering & Electronics,
2012, 23(2): 173–178.
内、基线间距不大于半波长的子阵间的旋转不变关 [9] Koupatsiaris D A, Karystinos G N. Efficient DOA, DOD,
系得到无模糊的粗估计结果。之后利用虚拟线阵 and target estimation for bistatic MIMO sonar[C]// 2013
间、基线较长的子阵间的旋转不变关系得到一组有 IEEE International Conference on Acoustics, Speech, and
Signal Processing ICASSP 2013. IEEE, 2013: 5155–5159.
模糊的精估计结果。最后参考粗估计结果对精估计
[10] 程雪, 王英民. 低复杂度的 MIMO 声呐协方差矩阵重构方
结果进行解模糊，得到高精度、无模糊的 DOA 估计 法 [J]. 应用声学, 2019, 38(4): 666–673.