Page 10 - 《应用声学》2021年第4期
P. 10
494 2021 年 7 月
仿真结果如图 2 所示,由于双尺度 ESPRIT 算 间距可以提高 DOA 估计性能,但也不宜将间距选
法解模糊时需要参考 ESPRIT 算法的粗估计结果, 择得过大,间距过大可能会损失部分虚拟阵元接
当SNR 较低时,ESPRIT算法估计精度已无法满足 收信号的信息,所以需要利用仿真实验确定合适
正确解模糊的要求,所以从图2中可以看出,当SNR 的子阵间距。在本实验条件下,认为当子阵间距
低于 −15 dB 时,双尺度 ESPRIT 算法估计误差与 ∆ 2 = 7d r 时算法 DOA 估计精度最高,所以在接下
ESPRIT 算法相近。随着 SNR 的增加,与 ESPRIT 来的仿真试验中双尺度降维 ESPRIT 算法精估计
算法相比,双尺度 ESPRIT 算法 DOA 估计均方误 时子阵间距选择∆ 2 = 7d r 。
差明显小于 ESPRIT 算法,认为加大子阵间距能够 图 4(a) 对比了 EPSRIT 算法、双尺度 EPSRIT
算法、降维 ESPRIT 算法、双尺度降维 EPSRIT 算
起到提高 DOA 估计精度的作用,且间距 ∆ 1 = 3d t
时性能最优。所以在接下来的仿真实验中双尺度 法和降维 MUSIC 算法 [26] 的 DOA 估计性能。可以
ESPRIT算法精估计时子阵间距选择∆ 1 = 3d t 。 看出随着 SNR 的增高,ESPRIT 算法和降维 ES-
之后评估了双尺度降维 ESPRIT 算法选择不 PRIT 算法的 DOA估计性能逐渐相近,且始终低于
同基线间距时的 DOA 估计性能。图 3 展示了子阵 双尺度类算法估计精度。双尺度降维 ESPRIT算法
间距 ∆ 2 = 3d r ∼ 13d r 时,角度估计均方根误差随 精度略高于双尺度 ESPRIT 算法。降维 MUSIC 算
SNR 的变化情况。从图 3 能够看出,适当拉大子阵 法在 SNR 低于 −10 dB 时,估计性能明显差于其他
几种算法,随着 SNR 的增高,估计精度与双尺度降
维 ESPRIT 算法相近。但值得注意的是,双尺度类
D/d r
10 1
D /d t
算法无法有效降低 SNR 门限,当 SNR 较低时,粗
D /d t
D /d t 估计结果的精度已无法满足正确解模糊的要求,导
RMSE/(°) 10 0 D /d t 致此时精估计结果精度也会很差。之后还评估了
D /d t
阵列流形误差对各算法 DOA 估计精度的影响,分
10 -1
别对接收阵列和发射阵列流形误差的影响进行分
析。图 4(b)∼ 图4(d)分别展示了发射阵元或接收阵
10 -2 元存在幅相扰动误差以及发射、接收阵元同时存在
-20 -15 -10 -5 0 5 10 15 20
SNR/dB 幅相扰动误差时,几种算法估计性能的变化情况。
假设图 4(b)∼ 图 4(d) 中发射阵元或接收阵元均满
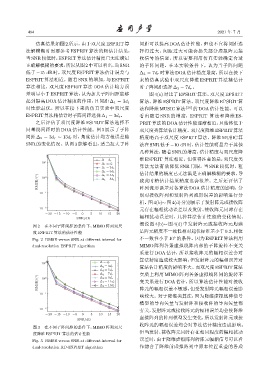
图 2 在不同子阵间距的条件下,MIMO 阵列双尺
度 ESPRIT 算法的估计性能 足阵元幅度不一致性相对起伏标准差小于0.2、相位
◦
Fig. 2 RMSE versus SNR at different interval for 不一致性小于 10 的条件。因为 ESPRIT 算法利用
dual-resolution ESPRIT algorithm MIMO 阵列各条虚拟线阵内部的子阵旋转不变关
系进行 DOA 估计,所以接收阵元的幅相误差会对
算法精度造成较大影响,但发射阵元的幅相误差对
10 1 D/d r
D /d r 算法估计精度的影响不大。而双尺度 ESPRIT算法
D /d r
D /d r 实质上利用 MIMO 阵列各条虚拟线阵间的旋转不
RMSE/(°) D /d r 变关系进行 DOA 估计,所以算法估计性能对接收
0
10
D /d r
D /d r
阵元的幅相误差不敏感,但受发射阵元幅相误差影
10 -1
响较大。对于降维类算法,因为降维虚拟线阵信号
模型的导向矢量与发射阵和接收阵的导向矢量都
10 -2 有关,发射阵元或接收阵元的幅相误差均会使降维
-20 -15 -10 -5 0 5 10 15 20
虚拟阵列的阵列模型发生变化,所以发射阵元或接
SNR/dB
收阵元的幅相误差均会对算法估计精度造成影响。
图 3 在不同子阵间距的条件下,MIMO 阵列双尺
度降维 ESPRIT 算法的估计性能 但当发射、接收阵元同时存在相同程度的幅相扰动
Fig. 3 RMSE versus SNR at different interval for 误差时,由于降维虚拟阵列的阵元幅相信号可以看
dual-resolution RD-ESPRIT algorithm 作综合了降维前虚拟阵列中原本位置重叠的各虚