Page 53 - 《应用声学》2021年第4期

第 40 卷 第 4 期 刘舒宁等： 压缩感知在宽带声学多普勒测速技术中的应用 537

比例提高，使用两种观测矩阵下的信号相关系数相 离散傅里叶变换基，使用 OMP 算法得到重构信
当且趋于稳定。因此，在下一步仿真实验中，选择离 号与原始信号时域和频域对比如图 4 所示。 此
散傅里叶基作为变换基和高斯随机矩阵作为观测 时，重构回波信号与原始回波信号的相关系数
矩阵。 大于 0.98，重构回波信号与原始信号具有很好的
当压缩比例为 0.4 时，选择高斯随机矩阵和 相关性。

1.0
ԔݽηՂ
0.5 ᧘౞ηՂ
ॆʷӑηՂࣨए -0.5 0

-1.0
0 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.10
௑ᫎ/ms
(a) ԔݽηՂˁ᧘౞ηՂ௑۫ฉॎࠫඋڏ
1.0 ԔݽηՂ
ॆʷӑηՂᮠ៨ࣨएፐࠫϙ 0.6
0.8
᧘౞ηՂ

0.4

0.2
0
0 0.2 0.4 0.6 0.8 1.0 1.2 1.4 1.6 1.8 2.0
ᮠဋ/MHz
(b) ԔݽηՂˁ᧘౞ηՂᮠ៨ࠫඋڏ

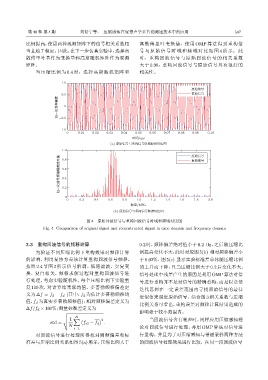
图 4 原始回波信号与重构回波信号时域和频域对比图
Fig. 4 Comparison of original signal and reconstructed signal in time domain and frequency domain

3.3 重构回波信号的频移计算 0.2 时，频移偏差绝对值小于 0.2 Hz，之后随压缩比
为验证不同压缩比例下重构效果对频移计算 例提高变化不大，此时对应图5(b) 相对频移偏差小
的影响，利用复协方差法计算重构回波信号频移。 于0.02%。图5(c) 显示实验标准差总体随压缩比例
按照 2.4 节图 2 所示信号解调、低通滤波、实复变 的上升而下降，且当压缩比例大于 0.2 后变化不大。
换、复自相关、频移求解过程对重构回波信号进 信号处理中残差产生的原因是利用 OMP 算法对信
行处理，考虑实验随机性，每个压缩比例下实验重 号进行重构并不是对信号的精确重构，而是以贪婪
复 100 次，对计算结果取均值。多普勒频移偏差定
迭代思想在一定误差范围内寻找原始信号的最佳
义为 ∆f = f d − f d (其中，f d 为估计多普勒频移均
近似值来逼近原始信号。结合图 3 相关系数与压缩
值，f d 为真实多普勒频移值)；相对频移偏差定义为
比例关系可看出，重构误差对频移计算结果造成的
∆f/f d × 100%；测量标准差定义为
影响处于较小范围内。
v
u N
1 ∑ ( ) 2 当回波信号含有噪声时，同样应用压缩感知理
u
std = t f di − f d .
N 论对回波信号进行处理，并用 OMP 算法对信号进
i=1
对回波信号进行处理所得相对测频偏差和标 行重构。并且为了对压缩感知与带通采样两种方法
准差与压缩比例关系如图 5(a) 所示，压缩比例大于 的回波信号处理效果进行比较，在同一段回波信号