Page 60 - 《应该声学》2022年第2期

228 2022 年 3 月

1.0 10
0
R S ↼τ↽ τ=τ p (x s )
0.8 R W ↼τ↽ 0.8
8
0.6 0.6
6
0.4
ࣨए Y/m 0.4
0.2 4
0.2
0
Ρ p (τ p ↼x↽)
2 0 0
τ p (x)=τ p (x s )
-0.2 τ p (x)=τ p (x s )
0
x s -0.2
0
-0.04 -0.02 0 0.02 0.04 0.06 0.08      
τ/s X/m
(a) GCCηՂ (b) Dτ p ↼x↽ᄊॖ־
0 0.16 0
⊲
0.14
⊲
0.12
⊲
0.10
-10 -10 ⊲
0.08
⊲
Y/m 0.06 Y/m ⊲
0.04
-20 -20 ⊲
0.02
⊲
0
⊲
ܦູͯᎶ -0.02 ܦູͯᎶ
ͥᝠͯᎶ ͥᝠͯᎶ 
-30 -30
       
X/m X/m
(c) ஙཥ஍ऄ (d) ေਇ౎͈ʾᄊSRPࠀͯ
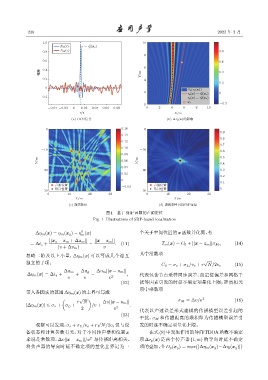
图 1 基于 SRP 函数的声源定位
Fig. 1 Illustrations of SRP-based localization

0
∆η m (x) = η m (x g ) − η (x) 个关于空间位置的x函数并化简，有
m
||x g − z m + ∆z m || ||x − z m ||
= ∆t s + − . (11) T m (x) = C 0 + ||x − z m ||σ M , (14)
(v + ∆v m ) v
忽略二阶及以上小量，∆η m (x) 可以写成几个相互 其中常数项
独立的子项： √
C 0 = σ s + σ L /v s + r N/2v s (15)
∆z m ∆z g ∆v m ||x − z m ||
∆η m (x) = ∆t s + + − , 代表包含节点采样同步误差、自定位偏差和网格干
v v v 2
(12) 扰等因素引发的时延不确定项量化上限；距离相关
项中乘数项
带入各因素的范围∆η m (x)的上界可写成
√ 2
( ) σ M = ∆v/v (16)
r N ∆v||x − z m ||
|∆η m (x)| 6 σ s + σ L + /v + .
2 v 2
代表以声速误差形式建模的传播模型误差引起的
(13)
干扰，σ M 和传播距离的乘积即为传播模型误差引
√
观察可以发现，σ s + σ L /v s + r N/2v s 仅与设 发的时延不确定项量化上限。
备状态和计算参数有关，对于不同传声器和位置 x 在式(8)中发生作用的导向TDOA函数不确定
2
来说是常数项，∆v||x − z m ||/v 与传播距离相关。 项 ∆τ p (x) 是两个传声器 {l, m} 的导向时延不确定
将传声器的导向时延不确定项的量化上界记为一 项的叠加，令D p (x g ) = max{|∆η m (x g )−∆η l (x g )|}