Page 65 - 《应该声学》2022年第2期

第 41 卷 第 2 期 黄毅伟等： 导向相应功率定位中时延不确定项的影响 233

100
͜ܦ٨ᓬག 20
50
0
Y/m 0 SNR/dB -20

-40
-50 ᄇ٪(Лࣜ) ᄇ٪(ᰴᤰ)
Პቻ(Лࣜ) Პቻ(ᰴᤰ)
-60
ᲚᲞ(Лࣜ) ᲚᲞ(ᰴᤰ)
-100
-100 -50 0 50 100 20 40 60 80
X/m ᡰሏ/m
(a) ᓬགѬ࣋ (b) ͜ܦ٨ᓬགࠄྭڏ (c) ଌஆη٪උ
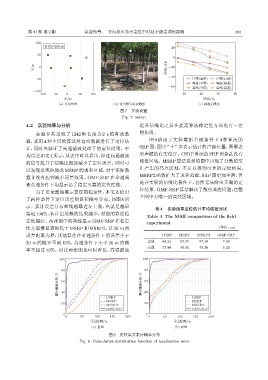
图 7 实验设置
Fig. 7 Setup
4.2 实验结果与分析 提升信噪比之后在提高算法稳定性方面也有一定
实验中共录取了 1242 帧长度为 2 s 的有效数 的作用。
据，采用 4 种不同的算法对这些数据进行了定位估 图 9 给出了实验数据全通条件下 4 种算法的
计，同时也验证了高通滤波处理下的定位结果。平 SRP 图，图中“十”字表示估计的声源位置，圆圈表
示声源的真实位置。CSRP算法的SRP图杂乱没有
均误差如表4 所示，从表中可以看出，经过高通滤波
峰值区域。MSRP算法得到的图中出现了分散的交
的信号提升了信噪比因此减少了定位误差。同时可
汇产生的亮点区域，不足以得到可靠的定位结果。
以发现单纯地修改 MSRP的求和区域，对于实际数
MSRP2 函数扩大了求和范围，SRP 图更加平滑，但
据并没有起到减小误差效果。GMF-SRP 在全通或
是在实验的信噪比条件下，仍然无法给出正确的定
者高通条件下均显示出了稳定可靠的定位性能。
位结果。GMF-SRP算法解决了散焦效应问题，在整
为了更全面地展示算法的稳定性，本文还给出
个图中有唯一的高亮区域。
了两种条件下定位误差的累积概率分布，如图 8 所
示。累计误差分布曲线越靠近左上角，也就是越早
表 4 实验结果定位估计平均误差对比
接近 100%，估计出发散的结果越少，对应的算法稳
Table 4 The MAE comparison of the field
定性越好。两张图中的曲线显示 GMF-SRP 在稳定 experiment
性方面要显著地优于 MSRP 和 MSRP2，以 20 m 的 (单位: m)
误差距离为界，其他算法在全通条件下的误差小于 CSRP MSRP MSRP2 GMF-SRP
20 m 的概率不到 15%，高通条件下小于 20 m 的概 全通 64.21 57.35 87.10 7.68
高通 57.80 49.05 49.26 5.23
率不超过 40%。对比两张图也可以看出，高通滤波
100 100

80 80
ግᝠഐဋѬ࣋/% 60 ግᝠഐဋѬ࣋/% 60

40
CSRP 40 CSRP
MSRP MSRP
20 20
MSRP2 MSRP2
GMF-SRP GMF-SRP
0 0
0 50 100 150 200 0 50 100 150 200
ឨࣀᡰሏ/m ឨࣀᡰሏ/m
(a) Лᤰ (b) ᰴᤰ
图 8 定位误差累计概率分布
Fig. 8 Cumulative distribution function of localization error