Page 70 - 《应该声学》2022年第2期

238 2022 年 3 月

气缸高度，L 为AB 长度；双转子压缩机的两个气 模态叠加法计算外围钣金的频率响应。整机有限元
AB
缸相位相差180 ，双转子压缩冷媒的扭转力矩为 模型假设为N 个自由度系统，得到动力学公式为 [6]
◦
{ } { }
M G = M g (θ) + M g (θ + π). (2) [M] ¨ x + [C] ˙ x + [K] {x} = {f} , (3)
其中，[M]为质量矩阵；[C]为阻尼矩阵；[K]为刚度
໏ྟ
矩阵；{f} 为激振力矩向量；{x} 为位移响应向量。
P s
A 模态向量矩阵 [Φ] 求解后，系统节点的位移响应可
以表示为 [7]
B
θ {x} = [Φ] {q} . (4)

ω 应用特征向量间的正交性，式(3)转化为
D
T
C [M p ] {¨ q} + [C p ] { ˙ q} + [K p ] {q} = [Φ] {f} , (5)
໔үᣁߕ
P θ
其中，[M p ]、[C p ]、[K p ] 称为模态质量矩阵、模态阻
尼矩阵、模态刚度矩阵，均为对角阵。将式 (11) 与
图 2 转子压缩机气缸力学原理图
式 (7) 联立，求解出各节点在激振力矩 {f} 下的位
Fig. 2 Dynamical schematic design of rotor com-
移响应。
pressor’s cylinder
2.2 钣金模态测试与振动响应计算
压缩机转动力矩随压缩机运转频率的变化曲
应用 LMS Test.lab 测试系统对整机框体开展
线，如图3所示。
模态测试，确定整机钣金框体在 175.3 Hz 附近存在
明显共振(如图4 所示)。建立整机有限元仿真模型，
4500 在压缩机本体气缸中心位置处施加绕压缩机本体
4000
ԍ᎖఻ᣁүҧᅾ/(NSmm) 3000 中心轴的转动力矩，具体数值见图3。钣金结构阻尼
3500
2500
设置为 0.05，应用模态叠加法计算整机的振动频率
2000
响应发现：172 Hz下的振动位移响应最大(如图5所
1500
1000
示)，振型与模态测试结果相符。通过模态测试与整
500
机频响计算结果对比，明确整机压缩机 5280 r/min
0
30 40 55 58 61 70 76 80 85 90 95 100 105 110 115
ԍ᎖఻ᤂᣁᮠဋ/Hz 运转时两倍频大主要是外围钣金框体共振引起的，
且计算频率偏差约 3 Hz，计算精度满足进一步开展
图 3 压缩机转动力矩曲线
各部件的声学贡献量分析的要求。
Fig. 3 Torque curve of compressor
2 钣金振动仿真

压缩机激振力通过铜管与底脚传递至空调室
外机钣金，引起钣金共振并辐射噪声。获得压缩机
两倍频扭矩后，施加在室外机空调系统整机有限元
模型上，应用模态叠加法，进一步计算整机钣金的振

动速度响应。

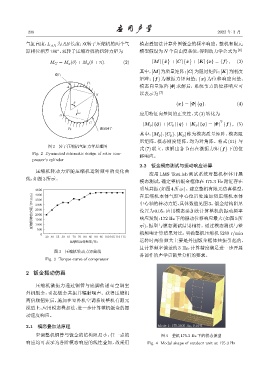
2.1 模态叠加法原理 Mode 1: 175.3505 Hz, 0.10%
空调整机铜管与钣金的结构阻尼小，任一点的 图 4 整机 175.3 Hz 下的模态振型
响应均可表示为各阶模态响应的线性叠加，故采用 Fig. 4 Modal shape of outdoor unit at 175.3 Hz