Page 66 - 《应该声学》2022年第2期

234 2022 年 3 月

100 100

50 50

Y/m 0 Y/m 0

-50 -50
ܦູͯᎶ ܦູͯᎶ
ͥᝠͯᎶ ͥᝠͯᎶ
-100 -100
-100 -50 0 50 100 -100 -50 0 50 100
X/m X/m
(a) CSRP (b) MSRP

100 100

50 50

Y/m 0 Y/m 0

-50 -50
ܦູͯᎶ ܦູͯᎶ
ͥᝠͯᎶ ͥᝠͯᎶ
-100 -100
-100 -50 0 50 100 -100 -50 0 50 100
X/m X/m
(c) MSRP2 (d) GMF-SRP

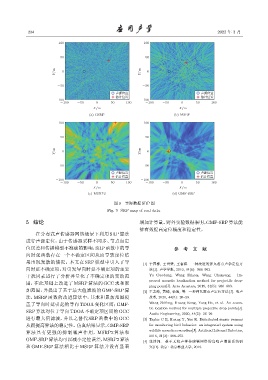
图 9 实际数据 SRP 图
Fig. 9 SRP map of real data

5 结论 增加计算量。野外实验数据表明，GMF-SRP算法能
够有效提高定位精度和稳定性。
在分布式声传感器网络场景下利用 SRP 算法
进行声源定位，由于传感器采样不同步、节点自定
位误差和传播模型不准确的影响，SRP 函数中的导 参 考 文 献
向时延函数存在一个不确定区间从而导致定位结
果出现发散的情况。本文在 SRP 模型中引入了导 [1] 于国栋, 王世赞, 王春阳. 一种改进的弹丸落点声学定位方
向时延不确定项，对引发导向时延不确定项的主要 法 [J]. 声学学报, 2019, 44(6): 986–993.
干扰因素进行了分析并量化了不确定项的变动范 Yu Guodong, Wang Shizan, Wang Chunyang. Im-
proved acoustic localization method for projectile drop-
围，在此基础上改进了 MSRP 算法的 GCC 求和累
ping point[J]. Acta Acustica, 2019, 44(6): 986–993.
加范围，并提出了基于最大值滤波的 GMF-SRP 算 [2] 王志峰, 黄嵘, 杨博, 等. 一种弹丸落点声定位方法 [J]. 电声
法，MSRP 函数的改进算法中，其求和累加范围覆 技术, 2020, 44(5): 26–29.
盖了导向时延引起的导向 TDOA 变化区间；GMF- Wang Zhifeng, Huang Rong, Yang Bo, et al. An acous-
tic location method for multiple projectile drop points[J].
SRP 算法对位于导向 TDOA不确定项区间的 GCC
Audio Engineering, 2020, 44(5): 26–29.
进行最大值滤波，并以之替代 SRP 函数中的 GCC [3] Taylor C E, Huang Y, Yao K. Distributed sensor swarms
从而提高算法的稳定性。仿真结果显示，GMF-SRP for monitoring bird behavior: an integrated system using
算法具有更强的抑制噪声作用，MSRP2 算法和 wildlife acoustics recorders[J]. Artificial Life and Robotics,
2016, 21(3): 268–273.
GMF-SRP算法均可以减小定位误差，MSRP2算法
[4] 张博闻. 基于无线声学传感器网络的鸟鸣声增强系统研
和 GMF-SRP 算法相比于 MSRP 算法并没有显著 究 [D]. 北京: 北京林业大学, 2019.