Page 62 - 《应该声学》2022年第2期

230 2022 年 3 月

2
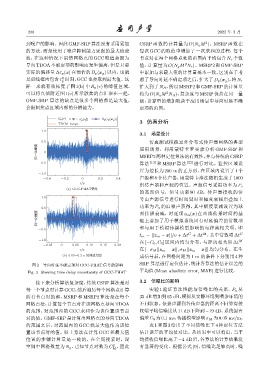
到噪声的影响。因此 GMF-SRP 算法没有采用累加 CSRP 函数的计算量为 O(N g M )。MSRP 函数在
的方法，而是使用了噪声抑制能力更强的最大值滤 每次 GCC 的取值中增加了一次求和的过程，每个
波，在这种情况下虽然网格点的 GCC 取值会因为 节点对在每个网格点处的范围内平均包含 N r 个数
2
导向 TDOA不确定项的影响而发生偏离，但是只要 值，计算量为 O(N g M N r )。MSRP2 和 GMF-SRP
实际的偏移量 ∆τ p (x) 在预估的 D p (x g ) 以内，也就 中累加与求最大值的计算量基本一致，区别在于考
是虚线框内包含τ 时刻，GCC也会取到最大值。这
0
p 虑了导向时延不确定项之后，扩大了 D p (x g )，将N r
样一来就有效拓宽了图 1(b) 中 R p (τ) 的峰值区域， 扩大到了 N R ，所以 MSRP2 和GMF-SRP 的计算量
可以将真值附近图 1(c) 所示散焦的点汇聚在一起。 约为 O(N g M N R )，复杂度与 MSRP 保持在同一量
2
GMF-SRP 算法的缺点是很多个网格都是最大值， 级，计算量的增加取决于应用场景中导向时延不确
会限制焦点区域内部的分辨能力。 定项的范围。

Ρ p (τ) Ρ p(τ p ) Ρ p(τ p(x g))
0
TDOA range 3 仿真分析
1.0
3.1 场景设计
0.5 仿真测试模拟室外分布式传声器网络的典型
ॆʷӑࣨए 0 应用场景，利用蒙特卡罗实验分析 GMF-SRP 和

MSRP2两种定位算法的有效性，并与传统的CSRP
-0.5 算法 [13] 和 MSRP 算法 [22] 进行对比。监控区域设
置为边长为 200 m 的正方形，在区域内设置了 1 个
-1.0
-0.4 -0.2 0 0.2 0.4 声源和 8 个传声器，用蒙特卡洛法随机生成了 1000
τ/s
组传声器和声源的位置。声源信号采用功率为 P s
(a) GCC-PHATηՂ
的高斯信号，信号功率 90 dB，传声器接收的信
1.0
号由声源信号进行时间延时和幅度衰减后叠加上
功率为 P n 的白噪声获得，其中幅度衰减设置为球
0.5
ॆʷӑࣨए 0 面传播衰减，时延项 η m (x) 在直线传播时间的基
础上叠加了用于模拟系统固有时延偏差的常数项

-0.5 和与用于模拟传播模型影响的与距离相关项，即
M
C
t m = ||z m − x||/v + ∆t + ∆t ，其中常数项 ∆t C
-1.0 M
在 [−C 0 , C 0 ] 区间内均匀分布，与距离相关项 ∆t
-0.05 0 0.05 0.10 0.15 0.20
τ/s 在 [−σ M ||z m − x||, σ M ||z m − x||] 均匀分布。在生
(b) 0.05~0.2 s ࡍᦊஊܸڏ 成信号后，在网格间距为 1 m 的条件下分别用 4 种
图 2 导向时延不确定项对 GCC-PHAT 信号的影响 SRP 算法进行定位估计，统计各算法的估计误差的
平均值(Mean absolute error, MAE)进行比较。
Fig. 2 Steering time delay uncertainty of GCC-PHAT

接下来分析算法复杂度，传统 CSRP 算法是对 3.2 信噪比的影响
每一个节点对计算GCC，然后遍历每个网格点计算 实验 1 验证算法性能与信噪比的关系，P n 从
所有节点对的和，MSRP 和 MSRP2 算法是在每个 35 dB增加到65 dB，模拟从安静环境到嘈杂环境的
网格点处，计算每个节点对在该网格点导向 TDOA 不同状态。依据声源到各传声器的距离不同算得接
的范围，对范围内的 GCC 求和作为该位置该节点 收端平均信噪比从11 dB下降到−19 dB。系统固有
对的值。GMF-SRP 是计算出网格点的导向 TDOA 偏差C 0 为0.1 ms，传播模型影响σ M 为0.05 ms/m。
的范围之后，对范围内的 GCC 找最大值作为该位 表 1 和图 3 给出了不同信噪比下 4 种定位方法
置该节点对的值。以上算法在计算 GCC 和最大值 估计误差的平均值对比。从结果中可以看出，当平
位置的步骤计算量是一致的，在全局搜索时，设 均接收信噪比高于 −4 dB 后，各算法的计算结果没
空间中网格数量为 N g ，已知节点对数为 C ，因此 有显著的变化。根据公式 (9)，信噪比足够高时，噪
2
M