Page 63 - 《应该声学》2022年第2期

第 41 卷 第 2 期 黄毅伟等： 导向相应功率定位中时延不确定项的影响 231

声项 R W (τ) 不影响信号分量 R S (τ) 在何时取到最 30 cm 和 3 m 的节点自定位误差，平均接收端信噪
大值，此时定位误差可以认为与信噪比无关。随着 比1 dB，σ M 为0.05 ms/m。
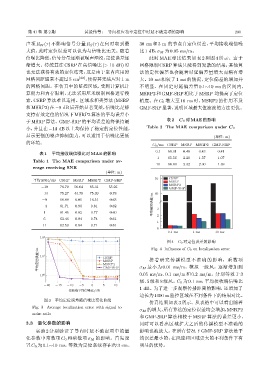
信噪比降低，信号分量逐渐被噪声湮没，定位误差逐 此时 MAE 对比结果如表 2 和图 4 所示。由于
渐增大。传统算法 CSRP 在高信噪比 (> 10 dB) 时 网格限制 CSRP 算法只能得到发散的结果，其他算
也无法获得有效的定位结果，这是由于室内应用时 法的定位偏差也会随着时延偏差量增大而稍有增
网格间距通常不超过5 cm [22] ，使得其无法应对1 m 大。10 ms 相较于 1 ms 的情况，定位偏差的增加并
的网格间距。在仿真中的监控区域，受到计算机计 不明显。在固定时延偏差量 0.1∼10 ms 的区间内，
算能力和内存限制，无法采用厘米级别网格进行搜 MSRP2和GMF-SRP 相比于 MSRP 均提高了定位
索，CSRP 算法难以适用。区域求和类算法 (MSRP 精度。在 C 0 增大至 10 ms 时，MSRP2 的作用不及
和MSRP2)在 −9 dB后开始显著变差，信噪比足够 GMF-SRP显著，说明区域最大值滤波的方法更优。
支持有效定位的情况下 MSRP2 算法的平均误差小
于MSRP 算法。GMF-SRP 的平均误差始终保持最 表 2 C 0 对 MAE 的影响
小，并且在 −14 dB 以上均保持了稳定的定位性能， Table 2 The MAE comparison under C 0
显示更强的噪声抑制能力，可以适用于信噪比更低 (单位: m)
的环境。 C 0 /ms CSRP MSRP MSRP2 GMF-SRP
0.1 59.01 0.48 0.43 0.41
表 1 平均接收端信噪比对 MAE 的影响
1 65.56 2.20 1.57 1.07
Table 1 The MAE comparison under av-
10 66.80 2.32 2.30 1.39
erage receiving SNR
(单位: m)
平均 SNR/dB CSRP MSRP MSRP2 GMF-SRP 70 CSRP
MSRP
MSRP2
−19 76.79 56.64 85.31 55.25
GMF-SRP
−14 75.27 44.78 75.39 0.78 60
−9 68.89 6.05 16.51 0.63
−4 61.71 0.90 0.81 0.62 ࣱکፐࠫឨࣀ/m 3
1 61.45 0.82 0.77 0.60 2
6 63.46 0.84 0.74 0.61
1
11 62.50 0.84 0.71 0.61
0
0.1 ms 1 ms 10 ms
10 2
图 4 C 0 对定位误差的影响
Fig. 4 Influence of C 0 on localization error
ࣱکࠀͯឨࣀ/m 10 1 CSRP σ M 最小为 0.01 ms/m，模拟一级风，逐渐增加到
接着研究传播模型不准确的影响，乘数项
MSRP
MSRP2

10 0 GMF-SRP 0.05 ms/m、0.1 ms/m 和 0.2 ms/m，分别等效于 3
级、5 级和 8 级风。C 0 为 0.1 ms，平均接收端信噪比
-20 -15 -10 -5 0 5 10
1 dB。为了进一步观察传播距离的影响，还增加了
ଌஆቫࣱکη٪උ/dB
边长为1000 m监控区域在不同条件下的结果对比。
图 3 平均定位误差随信噪比变化曲线
仿真结果如表 3 所示。从表格中可以看出随着
Fig. 3 Average localization error with signal to
σ M 的增大，所有算法的定位误差均会增加，MSRP2
noise ratio
和 GMF-SRP 算法相较于 MSRP 算法的误差更小，
3.3 量化参数的影响 同时可以看出区域扩大之后的传播模型不准确的
实验 2 分别验证了导向时延不确定项中的量 影响也被放大。在所有情况下 GMF-SRP 算法是平
化参数中常数项 C 0 和乘数项 σ M 的影响。首先设 均误差最小的，在风速和区域更大的不利条件下有
置 C 0 为 0.1∼10 ms，等效为定位系统存在约 3 cm、 明显的优势。