Page 153 - 《应用声学》2022年第3期

第 41 卷 第 3 期 徐洁等： 水声通信中基于均匀圆阵列的涡旋声波性能分析 475

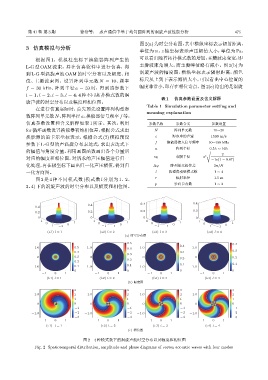
图 2(a) 为时空分布图，其中横纵坐标表示辐射距离，
3 仿真模拟与分析
单位为 m，z 轴坐标表示声压幅值大小，单位为 Pa，
根据图 1，模拟柱坐标下换能器阵列产生的 可以看出随着拓扑模式数的增加，主瓣波束变宽，即
L-G 型 OAM 波束，并在仿真软件中进行仿真，得 主瓣波束角增大，而主瓣峰值略有减小。图 2(b) 为
到 L-G 型涡旋声波 OAM 的时空分布以及幅度、相 涡旋声波的幅度图，横纵坐标表示辐射距离，颜色
位、主瓣波束图。设置阵列单元数 N = 10、频率 标尺从上到下表示幅值大小，可以看出中心位置的
f = 30 kHz、阵列半径 a = 3λ 时，得到该参数下 幅度非常小，即存在相位奇点。图 2(c)给出的是涡旋
l = 1、l = 2、l = 3、l = 4，4 种不同拓扑模式数的涡
表 1 仿真参数设置及含义解释
旋声波的时空分布以及幅度和相位图。
Table 1 Simulation parameter setting and
在进行仿真实际时，首先预先设置阵列构型参
meaning explanation
数阵列单元数N、阵列半径 a、换能器信号频率f 等，
仿真参数设置和含义解释如表 1 所示。其次，利用 参数名称 参数含义 参数设置
for循环函数设置换能器初始相位差，根据公式求出 N 阵列单元数 10∼20
换能器的笛卡尔坐标表示，根据公式 (7) 模拟预设 c 海水中的声速 1500 m/s
参数下 L-G 型的声涡旋分布表达式，求出表达式下 f 换能器接入信号频率 10∼150 kHz
a 阵列半径 0.5λ ∼ 10λ
的幅值与角度分量，利用画图函数画出各个分量所 √ 2
对应的幅度和相位图，对所求的声压幅值进行归一 w 0 束腰半径 a ∗ − ln(1 − 0.87)
化处理，再在极坐标下画出归一化声压幅值，得到归 ∆φ 阵列单元相位差 2π/N
一化方向图。 l 轨道角动量模式数 1 ∼ 4
图 2 是 4 种不同模式数 (模式数 l 分别为 1、2、 r 辐射半径 1.5 m
3、4) 下的涡旋声波的时空分布以及幅度和相位图。 p 径向节点数 1 ∼ 2

0.4 0.4 0.4
0.4
0.2 0.2 0.2 0.2
0 0 0 0
1 1 1 1
0 0 1 0 0 1 0 0 1 0 1
-1 -1 -1 -1 -1 -1 -1 -1 0
(a1) l=1 (a2) l=2 (a3) l=3 (a4) l=4
(a) ௑ቇѬ࣋ڏ
0.5 0.4
0.4
1.0 0.5 1.0 0.4 1.0 1.0
0.4 0.3 0.3
0.3
0 0.3 0 0 0.2 0 0.2
0.2
0.2
-1.0 0.1 -1.0 0.1 -1.0 0.1 -1.0 0.1
0 0 0 0
-1 0 1 -1 0 1 -1 0 1 -1 0 1
(b1) l=1 (b2) l=2 (b3) l=3 (b4) l=4
(b) ࣨएڏ
3 3 3 3
1.0 2 1.0 2 1.0 2 1.0 2
1 1 1 1
0 0 0 0 0 0 0 0
-1 -1 -1 -1
-1.0 -2 -1.0 -2 -1.0 -2 -1.0 -2
-3 -3 -3 -3
-1 0 1 -1 0 1 -1 0 1 -1 0 1
(c1) l=1 (c2) l=2 (c3) l=3 (c4) l=4
(c) ᄱͯڏ

图 2 4 种模式数下的涡旋声波时空分布以及幅度和相位图
Fig. 2 Spatiotemporal distribution, amplitude and phase diagrams of vortex acoustic waves with four modes