Page 156 - 《应用声学》2022年第3期
P. 156
478 2022 年 5 月
图6(b)为主瓣峰值的影响图,可见同等参数条件下, 主瓣峰值的变化趋势不明显。
模式下越高,主瓣峰值越小;而随着阵列半径的增 保持阵列半径 a = 3λ,设置频率 f = 30 kHz,
大,主瓣峰值减小,并且两种模式数下的减小趋势无 将换能器阵列单元数N ∈ [10, 20],依次仿真出轨道
明显差异。
角动量模式数 l = 1, 2, 3, 4 的 OAM 涡旋声波,记录
保持换能器阵列单元数N = 10,设置阵列半径
下4 种模式数的主瓣波束角和主瓣峰值随阵列单元
a = 3λ,频率从10 kHz增加到150 kHz,分别仿真出
数的变化趋势。图8(a)为阵列单元数对主瓣波束角
轨道角动量模式数 l = 1, 2, 3, 4 的 OAM 涡旋声波,
的影响图,能明显看到不同模式数的主瓣波束角不
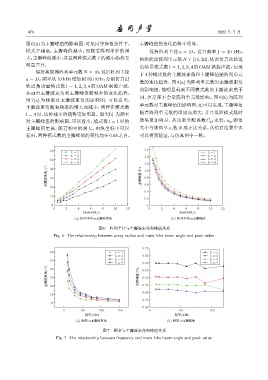
并画出主瓣波束角和主瓣峰值随频率的变化趋势。
同,但是都不会受阵列单元数影响。图 8(b) 为阵列
图 7(a) 为频率对主瓣波束角的影响图,可以看出,
单元数对主瓣峰值的影响图,还可以发现,主瓣峰值
主瓣波束角随着频率的增大而减小,同样在模式数
l = 4时,这种减小的趋势更加明显。图7(b) 为频率 随着阵列单元数的增加而增大,并且低阶模式数时
对主瓣峰值的影响图,可以看出,模式数 l = 1 时的 效果更加明显,从功率分配系数 C pl 来看,u lp 幅值
主瓣峰值更高,随着频率的增大,由纵坐标中可以 大小与阵列单元数 N 成正比关系,从仿真结果中也
看出,两种模式数的主瓣峰值的变化均在0.05 之内, 可以得到验证,与仿真图中一致。
60 1.6
L/ L/
L/ 1.4 L/
50 L/ L/
L/ 1.2 L/
˟ၥฉౌᝈ/(O) 30 ˟ၥϙ/Pa 1.0
40
0.8
0.6
20
0.4
10
0.2
0 0
0 2 4 6 8 10 12 0 2 4 6 8 10 12
ѵӧय़/λ ѵӧय़/λ
(a) ѵӧय़vs˟ၥฉౌᝈ (b) ѵӧय़vs˟ၥϙ
图 6 阵列半径与主瓣波束角和峰值关系
Fig. 6 The relationship between array radius and main lobe beam angle and peak value
0.70
60 L/ L/
L/ 0.65 L/
L/ L/
50
L/ 0.60 L/
˟ၥฉౌᝈ/(O) 30 ˟ၥϙ/Pa 0.55
40
0.50
0.45
20
0.40
10
0.35
0
0.30
0 50 100 150 0 50 100
ᮠဋ/kHz ᮠဋ/kHz
(a) ᮠဋvs˟ၥฉౌᝈ (b) ᮠဋvs˟ၥϙ
图 7 频率与主瓣波束角和峰值关系
Fig. 7 The relationship between frequency and main lobe beam angle and peak value