Page 164 - 《应用声学》2022年第3期

486 2022 年 5 月

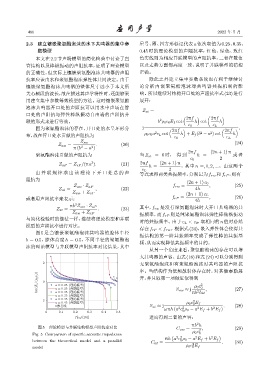
2.3 建立镶嵌聚氨酯泡沫的水下共鸣器的集中参 星号、圈、四方形标记代表 a 依次取值为 0.25、0.35、
数模型 0.45 时的理论模型的声阻抗率，红色、绿色、玫红

本文在 2.2 节声场模型的简化检验中讨论了直 色实线则为相应并联模型的声阻抗率，二者在数值
管结构以及棒纵振动的声阻抗率，证明了理论模型 以及走势方面都高度一致，说明了并联模型的猜想
的正确性，但实际上镶嵌聚氨酯泡沫共鸣器的声阻 正确。
抗率应该由水和聚氨酯泡沫弹性体共同决定。由于 除此之外建立集中参数系统也有利于继续讨
镶嵌聚氨酯泡沫共鸣器的整体尺寸远小于本文所 论分析内嵌聚氨酯泡沫对共鸣器共振机制的影
关心频段的波长，故在描述其声学特性时，还能够采 响。所以继续对结构开口处的声阻抗率式(23)进行
用建立集中参数等效模型的方法。这时镶嵌聚氨酯 展开：
泡沫共鸣器开口处的声阻抗可以用水中声场在管
Z st =
口处的声阻抗与弹性棒纵振动自由端的声阻抗并
( 2πf ) ( 2πf )
2
联的形式来进行等效。 b ρ 0 c 0 E f cot h cot h
因为聚氨酯泡沫的存在，开口处的水呈环形分 j ( 2πf ) c 0 c L ( 2πf ) ,
2
2
2
布，故在管口处水贡献的声阻抗为 ρ 0 c 0 a c L cot h + E f (b − a ) cot h
c 0 c L
Z sw (24)
Z aw = . (20)
2
2
π (b − a )
2πf (2n + 1) π
聚氨酯泡沫贡献的声阻抗为 当 Z st = 0 时， 得 到 h = 或 者
c 0 2
2
Z aP = Z sP /(πa ). (21) 2πf (2n + 1) π
h = ，其中 n =, 1, 2, ...。由这两个
c L 2
由 并 联 规 律 求 出 该 理 论 下 开 口 处 总 的 声 等式求得两类共振频率，分别记为f rw 和f rP ，则有
阻抗为
(2n + 1) c 0
f rw = , (25)
Z aw · Z aP
Z at = , (22) 4h
Z aw + Z aP
(2n + 1) c L
或者用声阻抗率来表示： f rP = 4h , (26)
2
πb Z aw · Z aP 其中，f rw 是没有聚氨酯泡沫时大开口共鸣器的共
Z st = . (23)
Z aw + Z aP
振频率，而 f rP 则是纯聚氨酯泡沫弹性棒做纵振动
与简化检验时的做法一样，继续将理论模型和并联
时的共振频率。由于 c L < c 0 ，取相同的 n 值时必然
模型的声阻抗率进行对比。
存在f rP < f rw 。根据式 (24)，嵌入弹性体会使得共
图 5 是当镶嵌聚氨酯泡沫共鸣器的腔体半径
振结构的第一阶共振频率变成了弹性棒的共振基
b = 0.5，腔体高度 h = 0.5，不同半径的聚氨酯泡
频，从而实现降低共振频率的目的。
沫的理论模型与并联模型声阻抗率对比结果，其中
从另一个角度来看，聚氨酯泡沫的存在可以增
大共鸣器的声容。由式(18)和式(24)可以分别得到
2 无聚氨酯泡沫和有聚氨酯泡沫时共鸣器的声阻抗
率。当结构作为低频散射体存在时，对其做泰勒展
Im(Z s/(ρ  c  )) 0 a/⊲ (ေ᝷വی) 开，并只取第一项做近似得到 2 0 , (27)
ρ 0 c
Z sw ≈ j
a/⊲ (ࣳᐏവی)
2
a/⊲ (ေ᝷വی)
a/⊲ (ࣳᐏവی) πb hω
-2 a/⊲ (ေ᝷വی) 2
a/⊲ (ࣳᐏവی) ρ 0 c E f
0
0ԠᏦጳ Z st ≈ j . (28)
2
2
2 2
ωπh (a c ρ 0 − a E f + b E f )
0 0.1 0.2 0.3 0.4 0.5 0
f♭c ⊳↼b↽♯ 进而得到二者的声容：
2
πb h
图 5 理论模型与并联结构模型声阻抗率对比 C aw = , (29)
ρ 0 c 2
Fig. 5 Comparison of specific acoustic impedance 0
( )
2 2 2 2
between the theoretical model and a parallel πh a c ρ 0 − a E f + b E f (30)
0
C at = 2 .
model ρ 0 c E f
0