Page 104 - 《应用声学》2022年第5期

780 2022 年 9 月

↼m x ֒m y ↽
↼m x֒m y↽ ↼m x֒m y↽
  
വरࣨए  വरࣨए  വरࣨए 

  

  
m x m x m x
m y m y m y
(a) X  ᄊ᠈࿹ (c) Y  ᄊ᠈࿹ (e) X+Yᄊ᠈࿹

↼m x ֒m y ↽
 ↼m x ֒m y ↽   ↼m x ֒m y ↽
വरࣨए  വरࣨए  വरࣨए 

  
  
m x m x m x
m y m y
(b) Xᄊ᠈࿹ (d) Yᄊ᠈࿹ (f) (X+Y)SZᄊ᠈࿹
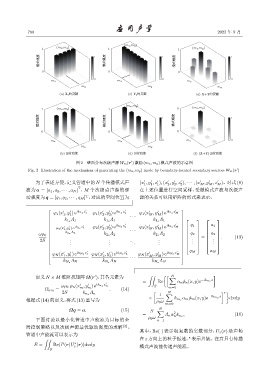
图 2 壁面分布次级声源 W m(r ) 激励 (m x, m y) 模式声波的示意图
′
′
Fig. 2 Illustration of the mechanism of generating the (m x, m y) mode by boundary-located secondary sources W m(r )
为了表述方便，定义管道中的 N 个传播模式声 (x , y , z ), (x , y , z ), · · · , (x , y , z )。对式(8)
′
′
′
′
′
′
′
′
′
1
2
M
2
M
2
M
1
1
T
波为 a = [a 1 , a 2 , · · · , a N ] ，M 个次级点声源的驱 在上述位置进行空间采样，受激模式声波与次级声
T
动强度为 q = [q 1 , q 2 , · · · , q M ] ，对应的空间位置为 源的关系可以用矩阵的形式来表示：
 ′ ′ ′ 
z
z
z
φ 1 (x , y ) e ik 1 z 1 φ 1 (x , y ) e ik 1 z 2 φ 1 (x , y ) e ik 1 z M
′
′
′
′
′
′
1 1 2 2 M M
· · ·
 
k 1 z Λ 1 k 1 z Λ 1 k 1 z Λ 1    
 
 z ′ z ′  q 1 a 1
′
′
′
′
z
φ 2 (x ,y ) e 2 2 M M    
 ′ ′ ik 2 z 1 ′ φ 2 (x , y ) e ik 2 z 2 φ 2 (x , y ) e ik 2 z M 
· · ·    
 1 1 
 k 2 z Λ 2 
k 2 z Λ 2 k 2 z Λ 2  q 2   a 2 
ωρ 0 
 (13)
. . . .  .   . 
.
.
    =   .
2S  . . . . . . . .   .   . 
 
   
 
  q M a N
′
z
z
z
 φ N (x , y ) e ik N z 1 φ N (x , y ) e ik N z 2 ′ φ N (x , y ) e ik N z M 

′ 
′
′
′
′
′
′
2
M
2
M
1
1
· · ·
Λ N Λ N Λ N
k N z k N z k N z
定义N × M 维阻抗矩阵Ω(r )，其各元素为 ∫∫ {[ N ]
′
∑
= Re α n ϕ n (x, y)e −ik n z z
′
z
ωρ 0 φ n (x , y ) e ik n z m S
′
′
Ω nm = m m . (14) n=0
2S k n z Λ n [ N ] }
∗
1 ∑ −ik m z z
根据式(14)的定义，将式(13)重写为 × ρ 0 ω k m z α m ϕ m (x, y)e dxdy
m=0
N
Ωq = a. (15) S ∑
2
= Λ n α k n z , (16)
n
下面讨论以最小化管道中声能流为目标的全 ρ 0 ω n=1
局控制策略以及次级声源最优驱动强度的求解 [3] 。
其中，Re( ) 表示取复数的实数部分，U z (r) 是声场
管道中声能流可以表示为
在z 方向上的粒子振速， 表示共轭。注意只有传播
∗
∫∫
∗
E = Re(P(r)U (r))dxdy
z 模式声波能传递声能流。
S