Page 106 - 《应用声学》2022年第5期

782 2022 年 9 月

的次级声源无法同时独立控制 (0, 0)、(0, 1) 和 (0, 2) 以上的频段取得 20 dB 以上的降噪量提升。该结果
这3 个n x = 0 的简并模式。同理可以解释空间分布 表明，次级声源沿着管道轴向分布时能更好地控制
(3) 的工作频率上限为 42.5 Hz 是因为无法独立控 高阶模式声波，在频率相对较高和高阶模式声波数
制 (0, 0) 和 (1, 0) 模式，而空间分布 (4) 的工作频率 目较多时对于控制效果的改进更为明显。
上限为85.0 Hz 是因为无法独立控制(0, 0)、(1, 0)和
(2, 0)三个简并模式。

ቇᫎѬ࣋ (1) ൓ጟܦູ

ቇᫎѬ࣋(1) ቇᫎѬ࣋(2)
1.0 m

ቇᫎѬ࣋ (2)
ቇᫎѬ࣋(3) ቇᫎѬ࣋(4)
1.0 m (a) ൓ጟܦູቇᫎѬ࣋
൓ጟܦູ
120
(a) ൓ጟܦູቇᫎѬ࣋
120 100
80
100 ܦ ᑟ ื /dB 60
ܦ ᑟ ื /dB 80 Ѻጟܦڤ 40 Ѻጟܦڤ

60
ቇᫎѬ࣋ (1)
ቇᫎѬ࣋ (1)
ቇᫎѬ࣋ (2) 20 ቇᫎѬ࣋ (2)
40
ቇᫎѬ࣋ (3) 0
ቇᫎѬ࣋ (4) 20 40 60 80 100 120 140 160 180 200
20 ᮠဋ/Hz
20 40 60 80 100 120 140 160 180 200
(b) ࠫऄᄊ٪ܦ଍҄஍౧
ᮠဋ/Hz
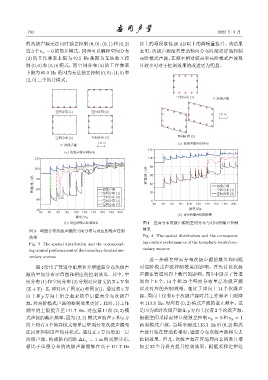
(b) ࠫऄᄊ٪ܦ଍҄஍౧ 图 4 壁面分布次级声源的空间分布与对应的噪声控制
图 3 壁面分布次级声源的空间分布与对应的噪声控制 效果
效果 Fig. 4 The spatial distribution and the correspond-
ing control performances of the boundary-located sec-
Fig. 3 The spatial distribution and the correspond-
ing control performances of the boundary-located sec- ondary sources
ondary sources
进一步研究壁面分布次级声源的数量和间距
图4 给出了管道中单层和多层壁面分布次级声 对高阶模式声波控制效果的影响。首先讨论次级
源的空间分布示意图和相应的控制效果。其中，空 声源在管道周向上数目的影响。图 5 中展示了管道
间分布(1)和空间分布(2)分别对应前文的X + Y和 周向上 6 个、14 个和 22 个壁面分布单层次级声源
(X + Y) · Z，即对应了图 2(e) 和图 2(f)。通过将x 方 以及对应的控制效果。相比于周向上 14 个次级声
向上和 y 方向上组合起来的单层壁面分布次级声 源，周向上仅有 6 个次级声源时其工作频率上限降
源，对高阶模式声波的控制效果更好。此时，其工作 至113.3 Hz，对应着(0, 2) 模式声波的截止频率。这
频率的上限提升至 141.7 Hz，对应第 11 阶 (2, 2) 模 是因为此时次级声源在 y 方向上仅有 2个次级声源，
式声波的截止频率，因为(2, 2) 模式声波在x 和y 方 根据空间采样定律只能独立控制 n y = 0 和 n y = 1
向上均有3 个简并模式而单层壁面分布次级声源无 两类模式声波，当频率超过 113.3 Hz 后 (0, 2) 模式
法同时控制这些简并模式。通过在 z 方向增加一层 声波开始在管道传播时，壁面分布次级声源将失去
次级声源，构成轴向间距 ∆L z = 1 m 的双层分布， 控制效果。但是，次级声源在管道周向上的数目增
相比于单层分布的次级声源能够在高于 141.7 Hz 加至 22 个并没有提升控制效果。根据采样定律这