Page 63 - 《应用声学》2022年第5期

第 41 卷 第 5 期 王寻等： 方波驱动下双气泡的动力学行为 739

൓Bjerknesҧ/(10 -4 N) -1 ൓Bjerknesҧ/(10 -4 N) -1
0
0

-2
-2
-3
-4 -3
-4
0 10 20 30 40 0 10 20 30
௑ᫎ/µs ௑ᫎ/µs
(a) f=25 kHz 0 (b) f=30 kHz

൓Bjerknesҧ/(10 -4 N) -1

-2
-3

-4
0 10 20
௑ᫎ/µs
(c) f=35 kHz
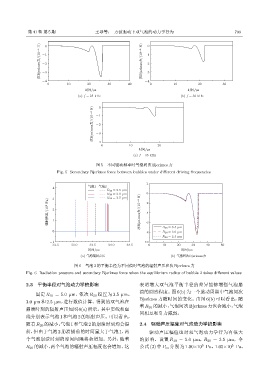
图 5 不同驱动频率时气泡间次 Bjerknes 力
Fig. 5 Secondary Bjerknes force between bubbles under different driving frequencies

2
ඡจ1 ඡจ2
4
R =3.5 µm
R =3.0 µm 0
R  =2.5 µm
3
ᣣ࠱ܦԍ/(10 8 Pa) 2 1 ൓Bjerknesҧ/(10 -4 N) -2
-4

0 -6 R 20 =3.5 µm
R 20 =3.0 µm
-8
R 20=2.5 µm
-1 -10
32.5 33.0 33.5 34.0 34.5 0 10 20 30 40 50
௑ᫎ/µs ௑ᫎ/µs
(a) ඡจᣣ࠱ܦԍ (b) ඡจᫎ൓Bjerknesҧ
图 6 气泡 2 的平衡半径为不同值时气泡的辐射声压和次 Bjerknes 力
Fig. 6 Radiation pressure and secondary Bjerknes force when the equilibrium radius of bubble 2 takes different values

2.3 平衡半径对气泡动力学的影响 表明增大双气泡平衡半径的差异能够增强气泡崩
溃的剧烈程度。图6(b)为一个脉动周期中气泡间次
固定 R 10 = 5.0 µm，依次 R 20 设置为 3.5 µm、
Bjerknes 力随时间的变化。由图 6(b) 可以看出，随
3.0 µm 和2.5 µm，进行数值计算。得到的双气泡在
着R 20 的减小，气泡间次Bjerknes力也会减小，气泡
崩溃时刻的辐射声压如图6(a) 所示。其中实线和虚
间相互吸引力减弱。
线分别表示气泡 1 和气泡 2 的辐射声压。可以看出，
随着R 20 的减小，气泡1和气泡2的崩溃时刻均会提 2.4 驱动声压幅度对气泡动力学的影响
前，但由于气泡 2 崩溃提前的时间量大于气泡 1，两 驱动声压幅值也对双气泡动力学行为有很大
个气泡崩溃时刻的时间间隔将会增加。另外，随着 的影响。设置 R 10 = 5.0 µm，R 20 = 3.5 µm，令
5
5
R 20 的减小，两个气泡的辐射声压幅度也会增加。这 公式 (3) 中 P us 分别为 1.00×10 Pa、1.05×10 Pa、