Page 64 - 《应用声学》2022年第5期

740 2022 年 9 月

5
5
1.10×10 Pa和1.15×10 Pa，数值计算后得到双气 大两个气泡崩溃的剧烈程度。从图 7(a) ∼ 图 7(d)，
泡半径随时间变化曲线如图 7 所示。图 8 展示了上 负声压阶段气泡的振荡次数逐步减少。在图7(a) 和
述驱动声压下的气泡的辐射声波。在图 7 和图 8 中， 图 7(b) 中，两个气泡几乎同时崩溃。但在图 7(c)中，
当 t ∈[0, 25 µs) 时，方波声压为负值，当 t ∈[25 µs, 气泡 1 的崩溃明显发生了延迟，此时气泡 2 比气泡 1
50 µs] 时，方波声压为正值。可以看出，随着驱动 更早崩溃。在图 7(d) 中，气泡 1 的崩溃被进一步延
声压的增大，两个气泡在膨胀时能达到的最大半径 迟，而气泡 2的崩溃也有所延迟，两个气泡崩溃的时
都有所增加。这意味着使用大幅度方波驱动可以增 间差有所减小。

80 80
ඡจ 1 ඡจ 1
ඡจ 2 ඡจ 2
60 60

ӧय़/µm 40 ӧय़/µm 40

20 20

0 0

0 10 20 30 40 50 0 10 20 30 40 50
௑ᫎ/µs ௑ᫎ/µs
5
5
(a) P us =1.00T10 Pa (b) P us =1.05T10 Pa
80 80
ඡจ 1 ඡจ 1
ඡจ 2 ඡจ 2
60 60

ӧय़/µm 40 ӧय़/µm 40

20 20

0 0

0 10 20 30 40 50 0 10 20 30 40 50
௑ᫎ/µs ௑ᫎ/µs
5
5
(c) P us =1.10T10 Pa (d) P us =1.15T10 Pa
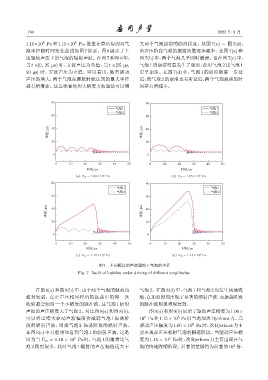
图 7 不同幅度的声波驱动下气泡的半径
Fig. 7 Radii of bubbles under driving of different amplitudes

在图 8(a) 和图 8(b) 中，由于两个气泡的脉动均 气泡 2。在图 8(d) 中，气泡 1 和气泡 2 均发生快速收
相对较弱，在正声压相回弹后的振荡中的每一次 缩，在崩溃时均出现了显著的辐射声波，而振荡阶段
收缩都会辐射一个小幅度的脉冲波，且气泡 1 辐射 的脉冲波则很难观察到。
声波的声压幅度大于气泡 2。对比图 8(a) 和图 8(b)， 图9(a)和图9(b)展示了驱动声压幅度为1.00×
可以看出增大驱动声波幅度会减弱气泡 1 振荡阶 10 Pa和1.15 × 10 Pa时气泡间次Bjerknes力。当
5
5
5
段的辐射声波，增强气泡 2 振荡阶段的辐射声波。 驱动声压幅度为1.00 × 10 Pa时，次Bjerknes 力主
在图 8(c) 中只能明显看到气泡 1 的辐射声波，这是 要出现在正压相时气泡的振荡阶段。当驱动声压幅
5
因为当 P us = 1.10 × 10 Pa 时，气泡 1 的崩溃比气 度为 1.15 × 10 Pa时，次Bjerknes力主要出现在气
5
4
泡 2 剧烈很多，此时气泡 1 辐射的声压幅值远大于 泡的快速收缩阶段。后者的量级约为前者的10 倍。