Page 69 - 《应用声学》2022年第6期

第 41 卷 第 6 期 李春阳等： 异构混合相关熵有源噪声控制算法 915

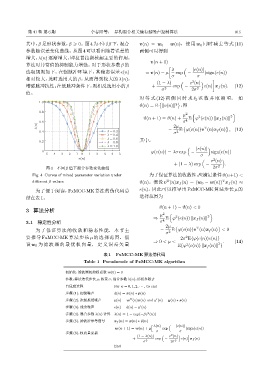
其中，β 是形状参数，β > 0。图 4 为不同 β 下，混合 v(n) = w 0 − w(n)，使用 w 0 同时减去等式 (10)
参数随误差变化曲线。从图 4 可以看出随着误差的 两侧可以得到
增大，λ(n) 逐渐增大，即拉普拉斯核起主要的作用，
v(n + 1)
算法对异常值的抑制能力增强。对于形状参数 β 的
[ (
λ |e(n)|
选取规则如下，在强脉冲环境下，其稳态误差 e(n) = v(n) − µ exp − )sign(e(n))
σ σ
相对较大，此时选用大的 β，从而得到较大的 λ(n)， ]
2
(1 − λ) ( e (n) )
增强脉冲抗性；在低脉冲条件下，则相反选用小的β + exp − e(n) x f (n). (12)
σ 2 2σ 2
值。
对 等 式 (12) 两 侧 同 时 求 ℓ 2 范 数 并 取 期 望， 如
1.0 { }
2
ϑ(n) = E ∥v(n)∥ ，得
0.8 2
µ { 2 2 }
ϑ(n + 1) = ϑ(n) + σ 4 E φ (e(n)) ∥x f (n)∥
λ↼n↽ 0.6 2µ { T }
0.4 λ/⊲ − σ 2 E φ(e(n))v (n)x f (n) , (13)
λ/⊲
λ/⊲ 其中，
0.2 λ/⊲
λ/⊲
( )
|e(n)|
0 φ(e(n)) = λσ exp − sign(e(n))
-5 -4 -3 -2 -1 0 1 3 3 4 5 σ
e↼n↽ ( 2 )
e (n)
+ (1 − λ) exp − 2 .
图 4 不同 β 值下混合参数变化曲线 2σ
Fig. 4 Curves of mixed parameter variation under 为了保证算法的收敛性，应满足条件ϑ(n+1) <
T
T
different β values ϑ(n)。假设 v (n)x f (n) = (w 0 − w(n)) x f (n) ≈
为了便于阅读，FxMCC-MK 算法的伪代码总 e(n)，因此可以推导出 FxMCC-MK 算法步长 µ 的
结在表1。 选择范围为
ϑ(n + 1) − ϑ(n) < 0
3 算法分析
µ 2 { 2 2 }
⇒ 4 E φ (e(n)) ∥x f (n)∥
3.1 稳定性分析 σ
2µ { T }
为了保证算法的收敛和稳态性能，本节主 − 2 E φ(e(n))v (n)x f (n) < 0
σ
要推导 FxMCC-MK 算法步长 µ 的选择范围。假 2σ E{φ(e(n))e(n)}
2
⇒ 0 < µ < . (14)
设 w 0 为滤波器的最优权向量， 定义误差矢量 E{φ (e(n)) ∥x f (n)∥ }
2
2
表 1 FxMCC-MK 算法伪代码
Table 1 Pseudocode of FxMCC-MK algorithm
初始化：滤波器初始权系数 w(0) = 0
参数：算法迭代步长 µ，核宽 σ，混合参数 λ(n)，形状参数 β
自适应过程 For n = 0, 1, 2, · · · , to end
步骤 (1)：初级噪声 d(n) = x(n) ∗ p(n)
步骤 (2)：次级抵消噪声 y(n) = w (n)x(n) and y (n) = y(n) ∗ s(n)
T
′
步骤 (3)：残余噪声 e(n) = d(n) − y (n)
′
步骤 (4)：混合参数 λ(n) 计算 λ(n) = 1 − exp(−βe (n))
2
步骤 (5)：滤波后参考信号 x f (n) = x(n) ∗ ˆ s(n)
[ λ(n) ( |e(n)|
w(n + 1) = w(n) + µ exp − )sign(e(n))
步骤 (6)：权向量更新 σ σ
2
(1 − λ(n)) ( e (n) ) ]
+ exp − e(n) x f (n)
σ 2 2σ 2
End