Page 70 - 《应用声学》2022年第6期

916 2022 年 11 月

3.2 计算复杂度对比 义公式如下 [20] ：
( )
在 ANC 的实际应用中，为了保证算法实时运 A e (n)
ANR(n) = 20 lg , (18)
算并降低硬件系统的负担，ANC 算法应当简单有 A d (n)

效。本文提出的算法与已有的算法计算复杂度对比  A e (n) = ηA e (n − 1) + (1 − η) |e(n)| ,
如表 2 所示。其中 L 表示控制滤波器抽头系数的个  A d (n) = ηA d (n − 1) + (1 − η) |d(n)| , (19)
数，M 表示用来估计次级路径模型的滤波器长度。
其中，η 是遗忘因子，η = 0.999；A e 和 A d 的初始值
从表 2 可以看出，相比于经典的 FxLMS 算法，本文
为0。
提出的算法只略微增加了计算量，为了获得更好
的鲁棒性能，增加的这些额外计算负担是完全可接 500
受的。
٪ܦࣨϙ 0

表 2 算法计算复杂度
-500
Table 2 Computational complexity of the 0.5 1.0 1.5 2.0 2.5 3.0 3.5 4.0
algorithms ٪ܦ᧔ನ/10 4
(a) α=1.6
算法 乘法/除法 加/减 指数 500
٪ܦࣨϙ 0
FxLMS 2L+2M+1 2L + 2M − 3 无
FxMCC 2L+2M+7 2L + 2M − 3 1

FxMMCC 2L+2M+17 2L+2M 3 -500
0.5 1.0 1.5 2.0 2.5 3.0 3.5 4.0
FxMCC-MK 2L+2M+18 2L+2M 3 ٪ܦ᧔ನ/10 4
(b) α=1.2
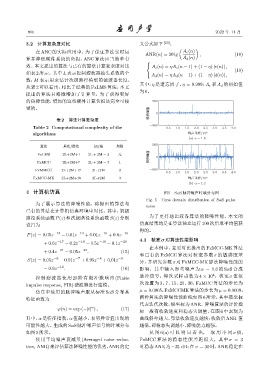
4 计算机仿真 图 5 SαS 脉冲噪声时域分布图

Fig. 5 Time domain distribution of SαS pulse
为了展示算法的降噪性能，将提出的算法与
noise
已有的算法在计算机仿真环境中对比。其中，初级
路径系统函数 P(z) 和次级路径系统函数 S(z) 分别 为了更好地比较各算法的降噪性能，本文的
设置为 仿真结果均是在算法独立运行 100次后取平均值获
得的。
P(z) = 0.05z −13 − 0.01z −14 + 0.01z −15 + 0.8z −16
4.1 核宽σ 对算法性能影响
−17 −18 −19 −20
+ 0.6z − 0.2z − 0.5z − 0.1z
在本例中，主要对比提出的 FxMCC-MK 算法
+ 0.4z −21 − 0.05z −22 . (15)
和已有的 FxMCC 算法对核宽参数 σ 的敏感度差
S(z) = 0.05z −6 − 0.01z −7 + 0.95z −8 + 0.01z −9
异，并研究参数 σ 对 FxMCC-MK 算法降噪性能的
− 0.9z −10 . (16) 影响。其中输入参考噪声为 α = 1.6 的 SαS 合成
4
脉冲信号，每次采样点数为 4 × 10 ，核宽 σ 值依
控制滤波器使用 20 阶有限冲激响应 (Finite
impulse response, FIR)滤波器进行建模。 次设置为 3、7、15、20、30，FxMCC 算法的步长为
仿真中使用的脉冲噪声服从标准 SαS 分布其 µ = 0.0005，FxMCCMK算法的步长为 µ = 0.0009。
特征函数为 两种算法的降噪性能曲线如图 6 所示，其中横坐标
代表迭代次数，纵坐标为 ANR。降噪算法的评价指
α
φ(n) = exp (−|t| ) , (17)
标一般有收敛速度和稳态失调量，在图 6 中表现为
其中，α 是特征指数，α 值越小，表明异常值出现的 曲线斜率越大，算法收敛速度越快；收敛后 ANR 值
可能性越大。生成的 SαS脉冲噪声信号的时域分布 越低，即稳态失调越小，降噪能力越强。
如图5所示。 从 图 6(a) 可 以 明 显 看 出， 取 用 不 同 σ 值，
使用平均噪声衰减量 (Averaged noise reduc- FxMCC 算法的稳态性能差距很大，其中 σ = 3
tion, ANR)来评估算法降噪性能的优劣，ANR的定 时稳态 ANR 为 −35 dB；在σ = 30 时，ANR 稳定在