Page 68 - 《应用声学》2022年第6期

914 2022 年 11 月

向量时，拉普拉斯核代价函数性能表面是高度非凸 混合系数的增加，拉普拉斯核的作用越明显，代价函
的，而高斯核接近最优值时表面为凸且平滑的，这意 数曲线在 [−2σ, 2σ] 区间内变化越尖锐，在区间外变
味着拉普拉斯核在最优解处性能远远不如高斯核， 化越平缓，这一变化特性对异常离群值有更好的抑
其非凸性甚至会导致陷入局部最优。 制效果。

2 FxMCC-MK算法 ⊲
⊲
2.1 FxMCC-MK算法代价函数
由第 1 节的分析可知，高斯核和拉普拉斯核的 J MK ↼n↽ ⊲ λ/
性能各有优劣。为了更好地增强相关熵算法的降 ⊲ λ/⊲
λ/⊲
噪能力，本文同时使用高斯核和拉普拉斯核组成混 λ/⊲
⊲ λ/⊲
合核，引入异构混合相关熵作为代价函数 [13] ，提出
FxMCC-MK算法。  ֓σ ֓σ  σ 2σ
FxMCC-MK 算 法 的 代 价 函 数 表 示 为 如 下 e↼n↽
形式： 图 3 不同混合程度下混合相关熵代价函数
[ ( )
|e(n)| Fig. 3 Mixture correntropy cost function under
J MK = 1 − E λ exp −
σ different mixing coefficients
( 2 ) ]
e (n)
+ (1 − λ) exp − , (8)
2σ 2 2.2 FxMCC-MK算法推导过程
其中，λ是混合系数，λ ∈ [0, 1]。 随机梯度是一种简单有效的在线求 ANC 最优
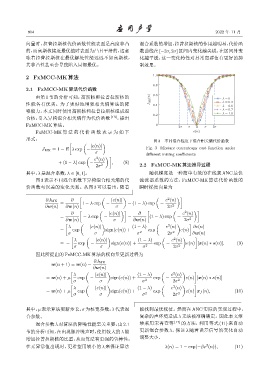
图3 表示不同混合系数下异构混合相关熵的代 滤波器系数的方法，FxMCC-MK 算法代价函数的
价函数与误差的变化关系。从图 3 可以看出，随着 瞬时梯度向量为

[ ( ) ( 2 )]
∂J MK ∂ |e(n)| e (n)
= 1 − λ exp − − (1 − λ) exp −
∂w(n) ∂w(n) σ 2σ 2
[ ( )] [ ( 2 )]
∂ |e(n)| ∂ e (n)
= − λ exp − − (1 − λ) exp −
∂w(n) σ ∂w(n) 2σ 2
[ ( ) ( 2 ) ]
λ |e(n)| (1 − λ) e (n) ∂e(n)
= exp − sign(e(n)) + exp − e(n)
σ σ σ 2 2σ 2 ∂w(n)
[ ( ) ( 2 ) ]
λ |e(n)| (1 − λ) e (n)
= − exp − sign(e(n)) + exp − e(n) [x(n) ∗ s(n)]. (9)
σ σ σ 2 2σ 2
因此所提出的FxMCC-MK算法的权向量更新过程为
∂J MK
w(n + 1) = w(n) −
∂w(n)
[ ( ) ( 2 ) ]
λ |e(n)| (1 − λ) e (n)
= w(n) + µ exp − sign(e(n)) + exp − e(n) [x(n) ∗ s(n)]
σ σ σ 2 2σ 2
[ ( ) ( 2 ) ]
λ |e(n)| (1 − λ) e (n)
= w(n) + µ exp − sign(e(n)) + exp − e(n) x f (n), (10)
σ σ σ 2 2σ 2

其中，µ表示算法更新步长，σ 为核宽参数，λ代表混 能找到最优权值。然而在 ANC 实际的实现过程中，
合参数。 复杂的声环境造成 λ无法被准确确定。因此本文继
混合参数 λ对算法的降噪性能至关重要，由2.1 续采用宋普查等 [17] 的方法，利用等式 (11) 来自动
节的分析可知，在出现脉冲噪声时，使用较大的 λ能 更新混合参数 λ，保证 λ 随着误差信号的变化自动
调整大小。
增加拉普拉斯核的比重，从而算法有更强的鲁棒性；
在无异常值出现时，更希望用较小的 λ 来保证算法 λ(n) = 1 − exp(−βe (n)), (11)
2