Page 20 - 《应用声学》2023年第1期

16 2023 年 1 月

在图 4中可以观察到明显的平流层通道与热层 行有效对比，排除单个大误差估计值对估计效果的
通道，当两种通道同时存在时，可以通过图中 A、B 过大影响。可以观察到 REDT 估计方法的平均误
区域内传播损失的均值分别作为平流层通道与热 差量小于 LANL 估计方法。在13 组实验数据中，有
层通道损失能量的估计值，记为 TL S 与 TL T ，单位 9 组数据使用 REDT 估计方法的误差更小，1 组数
为 dB。区域 A 为平流层通道与热层通道第一次分 据估计误差相似，3 组数据 LANL 估计方法误差较
离后，第一个平流层通道轨迹顶部的区域，用以估 小，相对误差关系见图5。
计此通道的能量数值。区域 B 为分离后第一个热
表 1 REDT 估计方法与 LANL 估计法效果对比
层通道轨迹顶部的区域，使用此区域估计热层通
Table 1 Comparison between REDT method
道能量的优点为，相比于在分离后在平流层顶高
and LANL method
度附近的热层轨迹区域，此区域可以计及热层高
度的水平风速对入射至热层的入射角的影响。由 序 声源 LANL LANL 估计 REDT REDT 估计
于 TL S 与 TL T 均为能量取对数后的值，因此使用 号 能量 估计值 误差 估计值 误差
1 24.4 27 0.0439 13.5 0.2561
TL = TL S − TL T 作为通道修正因子，用以修正大
2 0.2 5.3 1.4212 1.72 0.9355
气参数对远距离接收到声压幅度的影响。
3 42.7 188.3 0.6444 29 0.1679
根据上述大气中的声波传播衰减模型与传统
4 0.019 0.0196 0.0135 0.0134 0.1516
数据处理方法，结合衰减关系式 (9)，可以建立以下
5 0.019 0.0326 0.2345 0.0263 0.1412
模型：
6 0.096 0.582 0.7825 0.295 0.4880
B
2
A · P Z 10 C·TL = 1. (13) 7 0.096 0.705 0.8662 0.384 0.6015
8 0.096 0.130 0.1303 0.071 0.1310
对方程(13)两侧做对数处理得到：
9 0.096 0.087 0.0448 0.044 0.3368
lg A + B · lg P + 2 lg Z + C · TL = 0, (14) 10 0.0768 1.39 1.2587 0.467 0.7843
11 0.0768 1.33 1.2371 0.452 0.7693
其中，A、B、C 分别为待定半经验系数，通过实际测
12 0.0768 2.22 1.4603 1.07 1.1441
量数据拟合获得。
13 0.0768 0.91 1.0728 0.53 0.8369
本文使用来自美国 NTS 实验与美国 Sayarim
平均误差量 0.6859 0.5616
实验的数据集，确定等式 (14) 中的声压幅度衰减模
型系数，整理后获得以下声源能量估计方法：
10 3
2
W = 2.76 × 10 −6 · P 1.478 · R · 10 −0.0168·TL . (15) LANL
REDT
10 2
3 实验验证
10 1
由于本方法仅适用于平流层通道与热层通道 ᑟ᧚/kt
同时存在的声波传播模式，则使用数据集中满足条 10 0
件的 13 条数据将 LANL 提出的声源能量估计方法
10 -1
与本文提出的大气声传播通道声源能量估计方法
进行对比，LANL的估计方法为
10 -2
10 -2 10 -1 10 0 10 1 10 2 10 3
2
W = 1.105 × 10 −5 · P 1.47 · R · 10 −0.0279v c , (16) ᑟ᧚/kt
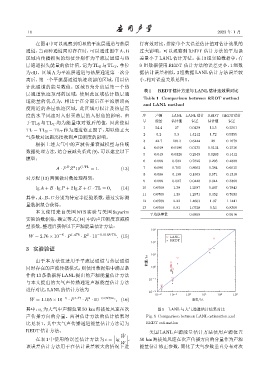
其中，v c 为大气中声源位置 50 km 海拔处风速在次 图 5 LANL 与大气通道估计结果对比
声传播方向的分量。两种估计方法的估计结果对 Fig. 5 Comparison between LANL estimation and
比见表 1，其中大气声传播通道能量估计方法记为 REDT estimation
REDT估计方法。 美国 LANL 声源能量估计方法使用声源位置
ˆ
在表 1 中使用的误差估计方法为 e = lg W ， 50 km海拔处风速在次声传播方向的分量作为声源

W
该误差估计方法用于在估计误差较大的情况下进 能量估计修正参数，简化了大气参数垂直分布对次