Page 9 - 《应用声学》2023年第1期

第 42 卷 第 1 期 李枚锖等： 两扬声器虚拟声重放的双耳声压控制与定位性能 5

过去的分析以及采用不同张角的扬声器进行分频 情况下，在1.3 kHz 以下，θ 1 = −30 、θ 2 = 30 对称
◦
◦
段重放 (最佳源分布) 而改善重放稳定性的研究相 扬声器布置的条件数最小；θ 1 = −15 、θ 2 = 30 的
◦
◦
符合 [11] 。 扬声器布置次之；θ 1 = 0 、θ 2 = 30 的扬声器布置
◦
◦
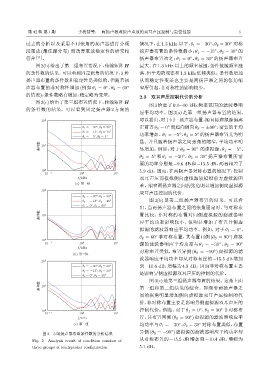
图2(b)给出了第二组布置情况下，传输矩阵 H 最大。在1.3 kHz 以上的频率范围，条件数随频率涨
的条件数的结果。可以看到固定张角的情况下，3 种 落，但平均的规律和1.3 kHz低频类似。条件数增加
扬声器布置的条件数和稳定性是类似的，但随着扬 从而稳定性变差也主要是两扬声器之间的张角缩
声器布置的非对称性增加 (例如 θ 1 = 0 、θ 2 = 60 ◦ 窄所引起，非对称性的影响较少。
◦
的情况)，条件数略有增加，稳定略为变差。 2.3 双耳声压控制代价的分析
图2(c)给出了第三组布置情况下，传输矩阵 H
图 3 给出了 0.1∼10 kHz 频率范围的滤波器响
的条件数的结果。可以看到固定扬声器 2 方向的
应平均功率。图 3(a) 是第一组扬声器布置的结果。
10 2 可以看出，对于同一扬声器布置，随目标虚拟源偏离
◦
◦
θ =-30° θ =30° 正前方 θ S = 0 而趋向侧向θ S = ±90 ，需要的平均
θ  =-15° θ  =15°
功率增加。θ 1 = −5 、θ 2 = 5 的扬声器布置尤为明
◦
◦
θ  =-5° θ  =5°
౎͈஝ 10 1 显。并且随着扬声器之间张角的缩窄，平均功率明
显增加。例如，对于 θ S = 90 的虚拟源，θ 1 = −5 、
◦
◦
θ 2 = 5 和 θ 1 = −30 、θ 2 = 30 扬声器布置所需
◦
◦
◦
要的功率分别是 −9.6 dB 和−15.5 dB，两者相差了
10 0 5.9 dB。因而，在两扬声器对称布置的情况下，控制
10 -1 10 0 10 1
f/kHz 双耳声压而模拟侧向虚拟源较模拟前方虚拟源困
(a) ኄʷጸ
难。缩窄两扬声器之间的张角明显增加侧向虚拟源
10 2
双耳声压控制的代价。
θ  =-30° θ  =30°
θ  =-15° θ  =45° 图 3(b) 是第二组扬声器布置的结果。可以看
θ  =0° θ  =60°
出，当两扬声器布置之间的张角固定时，与对称布
౎͈஝ 10 1 置比较，非对称的布置对同侧虚拟源的滤波器响
应平均功率影响较小，但明显增加了布置异侧虚
拟源的滤波器响应平均功率。例如，对于 θ 1 = 0 、
◦
θ 2 = 60 非对称布置，其布置同侧 (θ S = 90 ) 虚拟
◦
◦
10 0
10 -1 10 0 10 1 源的滤波器响应平均功率与 θ 1 = −30 、θ 2 = 30 ◦
◦
f/kHz
对称布置类似，布置异侧 (θ S = −90 ) 虚拟源的滤
◦
(b) ኄ̄ጸ
波器响应平均功率却从对称布置的 −15.5 dB 增加
10 2
到 −10.6 dB，增幅为 4.9 dB。因而非对称布置主要
θ  =-30° θ  =30°
θ  =-15° θ  =30° 是影响异侧虚拟源双耳声压的控制的代价。
θ  =0° θ  =30°
图3(c)是第三组扬声器布置的结果。这是上面
౎͈஝ 10 1 第一组和第二组结果的综合。即缩窄两扬声器之
间的张角明显增加侧向虚拟源双耳声压控制的代
价，非对称布置主要是影响异侧虚拟源双耳声压的
◦
◦
10 0 控制代价。例如，对于 θ 1 = 0 、θ 2 = 30 非对称布
10 -1 10 0 10 1
◦
f/kHz 置，其布置同侧 (θ S = 90 ) 虚拟源的滤波器响应平
◦
◦
(c) ኄʼጸ 均功率与 θ 1 = −30 、θ 2 = 30 对称布置类似，布置
◦
图 2 3 组扬声器布置条件数的分析结果 异侧 (θ S = −90 ) 虚拟源的滤波器响应平均功率却
Fig. 2 Analysis result of condition number of 从对称布置的 −15.5 dB 增加到 −10.4 dB，增幅为
three groups of loudspeaker configuration 5.1 dB。