Page 114 - 《应用声学》2023年第2期

302 2023 年 3 月

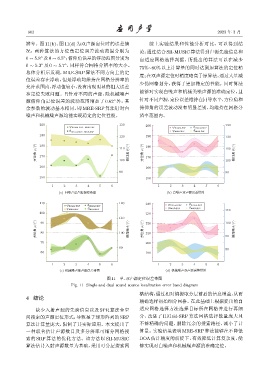
辨率。图 11(b)、图 11(d) 为双声源定位时的误差情 综上实验结果和性能分析对比，可以得到结
况，两种算法的方位角定位误差波动范围分别为 论：通过结合 SH-MUSIC 算法得到声源先验信息和
0 ∼ 5.8 及0 ∼ 6.5 ；俯仰角误差的浮动范围分别为 自适应网格选择判据，所提出的算法可以在减少
◦
◦
0 ∼ 5.3 及 0 ∼ 5.7 ，同样符合网格分辨率的大小。
◦
◦
75%∼80% 以上计算量的同时达到原算法的定位精
总体分析后发现，MRE-SRP 算法不同方向上的定
度；在双声源定位时精度略高于原算法，通过大量减
位误差存在浮动，但是浮动均维持在网格分辨率的
少伪网格划分，获得了更加稳定的性能。同时算法
允许范围内，浮动值较小，没有出现明显的粗大误差
能够对实现白噪声和机械类噪声源的准确定位，且
和定位失败问题。且针对不同的声源，除机械噪声
源俯仰角定位误差的波动范围增加了 0.62 外，其 针对不同声源，定位误差维持在同等水平，方位角和
◦
余参数的波动基本相同，即 MRE-SRP 算法针对白 俯仰角的误差波动没有明显差别，均维持在网格分
噪声和机械噪声源均能实现稳定的定位性能。 辨率范围内。
200 130 200 130
ϕ HiGrid-SRPnjMRE-SRP
ϕ HiGrid-SRP θ HiGrid-SRP
θ HiGrid-SRPnjMRE-SRP ϕ MRE-SRP θ MRE-SRP
190 120 190 120
வͯᝈ ϕ/(O) 180 110 ο̈́ᝈ θ/(O) வͯᝈ ϕ/(O) 180 110 ο̈́ᝈ θ/(O)

170
170
160 100 160 100
90 90
150 150
1 2 3 4 5 6 1 2 3 4 5 6
(a) ᄇ٪ܦӭܦູឨࣀࣜڏ (b) ᄇ٪ܦԥܦູឨࣀࣜڏ

110 120 240
ϕ HiGrid-SRP θ HiGrid-SRP ϕ HiGrid-SRP θ HiGrid-SRP
ϕ MRE-SRP θ MRE-SRP
ϕ MRE-SRP θ MRE-SRP
110
100 230
110 220 100
வͯᝈ ϕ/(O) 80 100 ο̈́ᝈ θ/(O) வͯᝈ ϕ/(O) 210 90 ο̈́ᝈ θ/(O)
90

70 200
90
80
60 190

1 2 3 4 5 6 1 2 3 4 5 6
(c) ఻೚٪ܦӭܦູឨࣀࣜڏ (d) ఻೚٪ܦԥܦູឨࣀࣜڏ

图 11 单、双声源定位误差带图
Fig. 11 Single and dual sound source localization error band diagram

格结构，通过相对熵提取分层前后的信息增益，从而
4 结论
精确选择初始细分网格。在此基础上根据提出的自
缺少入射声源的先验信息以及 SPR 算法全空 适应网格选择方法选择目标所在网格并进行再细
间搜索的声源定位形式，导致基于球形阵列的 SRP 分，改进了 HiGrid-SRP 算法网格选择数量庞大且
算法计算量庞大，限制了其实际应用。本文提出了 不够精确的问题，删除冗余的搜索路径，减小了计
一种联合估计声源数目及多分辨率可细分网格搜 算量。实验结果表明 MRE-SRP 算法能够在不降低
索的 SRP 算法的优化方法。该方法以 SH-MUSIC DOA 估计精度的前提下，有效降低计算复杂度，能
算法估计入射声源数量为基础，采用可分层搜索网 够实现对白噪声和机械噪声源的准确定位。