Page 111 - 《应用声学》2023年第2期

第 42 卷 第 2 期 李睿林等： 球形阵列自适应网格分层定位算法 299

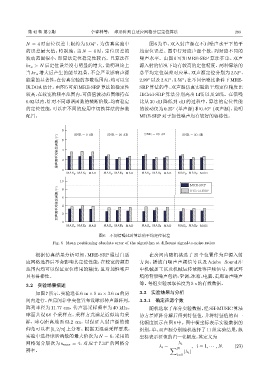
N = 4 时定位误差上限约为 5.04 ，为仿真实验中 图 6 为单、双入射声源在不同噪声水平下的平
◦
的误差最大值；特别地，当 N = 6 时，定位误差的 均定位误差。图中行对应声源个数，列对应不同的
波动范围很小，即算法定位稳定性较高。且算法在 噪声水平。由图 6 可知 MRE-SRP 算法在单、双声
kr a > N 后定位误差没有明显的增大，说明理论上 源入射的情况下均有较高的定位精度。两种算法的
当 kr a 增大后产生的能量混叠，不会严重影响声源 总平均定位误差对应单、双声源定位分别为 2.52 、
◦
能量的显著性，在仿真实验的参数范围内，均可以实 2.99 以及2.81 、3.56 ；在不同信噪比条件下MRE-
◦
◦
◦
现DOA估计。由图5可知MRE-SRP算法的稳定性 SRP 算法的单、双声源仿真实验的平均定位精度比
较高，在较宽的频率范围内，可信值波动范围维持在 HiGrid-SRP 算法分别高出 14% 以及 20%。在信噪
0.02以内，针对不同球谐函数的截断阶数，均有稳定 比从 30 dB 降低到 dB 的过程中，算法的定位性能
的定位性能，可以在不同的应用中切换算法的参数 的波动仅为 0.25 (单声源) 和 0.46 (双声源)，说明
◦
◦
配置。 MRE-SRP对于加性噪声均有较好的鲁棒性。

8 6 SNR=0 dB SNR=10 dB SNR=20 dB SNR=30 dB
ӭܦࣱູکࠀͯឨࣀ/(O) 4 2

0
MAE ϕ MAE θ MAE MAE ϕ MAE θ MAE MAE ϕ MAE θ MAE MAE ϕ MAE θ MAE
10
MRE-SRP
ԥܦࣱູکࠀͯឨࣀ/(O) 6 4
8
HiGrid-SRP

0 2
MAE MAE MAE MAE
MAE ϕ MAE θ MAE ϕ MAE θ MAE ϕ MAE θ MAE ϕ MAE θ
图 6 不同信噪比时算法的平均定位误差
Fig. 6 Mean positioning absolute error of the algorithm at different signal-to-noise ratios

根据仿真结果分析可知，MRE-SRP 通过自适 在房间内随机挑选了 25 个位置作为声源入射
应网格选择后不会影响其定位性能，在较宽的频带 方向，播放白噪声声频信号以及 Adobe_Sound 库
范围内均可以保证定位结果的精度，且对加性噪声 中机械加工以及机械运转故障等声频信号，测试环
具有鲁棒性。 境的背景噪声包括：空调、冰箱、电脑、走廊语声噪声
3.2 实验场景描述 等。每组实验录取长度为5 s的有效数据。
如图7 所示，实验选在 6 m × 5 m × 3.6 m的房 3.3 实验结果与分析
间内进行。在房间靠中央位置布设球形传声器阵列， 3.3.1 确定声源个数
阵列半径为 11.77 cm，传声器采样频率为 40 kHz。 随机选取了部分实验数据，经SH-MUSIC 算法
球面共设 64 个采样点，采样方式满足近似均匀采 协方差矩阵分解后得到特征值，并将特征值的归一
样，球心距离地面 63.2 cm，以保证入射声源的俯 化幅度展示在图 8 中。图中横坐标表示实验数据的
仰角可以在 [0, 2/π] 上分布。根据无混叠采样要求， 组别，单、双声源分别随机选择了11组实验结果，纵
实验中选择球谐函数的最大阶次为 N = 6，采用的 坐标表示征值的归一化幅度，其定义为
网格划分层次为 u max = 4，对应于 7.33 的网格分 λ i
◦
λ i = , i = 1, · · · , N. (23)
辨率。 ∑ N
|λ i |
i=1