Page 112 - 《应用声学》2023年第2期

300 2023 年 3 月

7300HQ CPU 2 2.50GHz 的计算机上编程实现并
运行。
与HiGrid-SRP算法相比，MRE-SRP以判断声
源个数作为算法的第一步，从表 1、表 2 可以看到改
进算法的显著优势：由已知的声源数来确定初始网
格的选择个数，避免了选择大量无关的网格，这样不
(a) ࠄᰎڤఀ (b) ᫼ѵ࣋ஊ
仅可以降低算法的计算量，且减少了伪网格的选择，
图 7 实验场景图
保证了算法DOA估计的精度。
Fig. 7 Experimental scene diagram
表 1 单声源定位时原算法和改进算法网格选择情况
0.6 ...
λ 
λ  λ N Table 1 Grid selection of the original al-
0.5
λ 
ॆʷӑྲढ़ϙ λ i 0.4 single sound source localization
gorithm and the improved algorithm for
0.3
细分个数/个
选中网格/个
备选网格/个
0.2 原算法 改进后 原算法 改进后 原算法 改进后 网格层次
12 12 7.6 1 u = 1
0.1
48 48 18.7 1.6 30.4 4 u = 2
121.6 16 3.8 1.2 74.8 6.4 u = 3
(a) ӭܦູ
299.2 25.6 15.2 4.8 u = 4
0.5
λ  λ  λ  ... λ N 表 2 双声源定位时原算法和改进算法网格选择情况
0.4
ॆʷӑྲढ़ϙ λ i 0.3 Table 2 Grid selection of the original al-
gorithm and the improved algorithm for
dual sound source localization
0.2
备选网格/个 选中网格/个 细分个数/个
0.1 网格层次
原算法 改进后 原算法 改进后 原算法 改进后
12 12 8.4 2 u = 1
(b) ԥܦູ 48 48 25.3 2.9 33.6 8 u = 2
134.3 32 7.5 4 101.2 13.2 u = 3
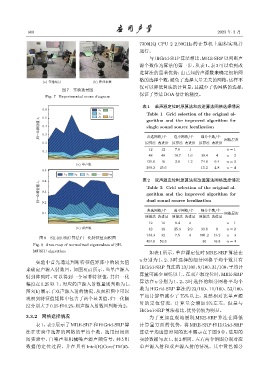
图 8 SH-MUSIC 算法归一化特征值面积图
404.8 52.8 30 16.8 u = 4
Fig. 8 Area map of normalized eigenvalues of SH-
MUSIC algorithm 如表 1 所示，单声源定位时 MRE-SRP 算法在
u 分别为 1、2、3 时选择的细分网格平均个数只有
实验中首先通过判断特征值矩阵中的较大值
HiGrid-SRP 算法的 13/100、8/100、31/100，平均计
来确定声源入射数目。如图 8(a) 所示，当单声源入
算量可减少80%以上。在双声源定位时，MRE-SRP
射到阵列时，可以得到一个显著特征值，其归一化
算法在 u 分别为 1、2、3 时选择的细分网格平均个
幅度在 0.25 以上，对应的声源入射数量则判断为 1；
数为 HiGrid-SRP 算法的 23/100、11/100、53/100，
图 8(b) 展示了双声源入射的情况，从面积图中可以
平均计算量减少了 75% 以上，虽然相对比单声源
观察到特征值矩阵中包含了两个显著值，归一化幅
时的定位情况，计算量会增加 5% 左右，但是与
度分别大于0.15和0.25，则声源入射数目判断为2。
HiGrid-SRP算法相比，优势仍较为明显。
3.3.2 网格选择情况 为了更加直观地展现 MRE-SRP 算法在降低
表 1、表 2 展示了 MRE-SRP 和 HiGrid-SRP 算 计算量方面的优势，将 MRE-SRP 和 HiGrid-SRP
法在实验中选择的网格的平均个数。选用封闭房 算法平均运算时间的比率展示在了图 9 中，选用的
间实验中，白噪声和机械噪声源声频信号，共 5 组 实验数据与表 1、表2 相同。左右两个饼图分别对应
数据的定位过程，并在具有 Intel(R)Core(TM)i5- 单声源入射和双声源入射的情况。其中黄色部分