Page 110 - 《应用声学》2023年第2期

298 2023 年 3 月

/ ∑ s↼k↽
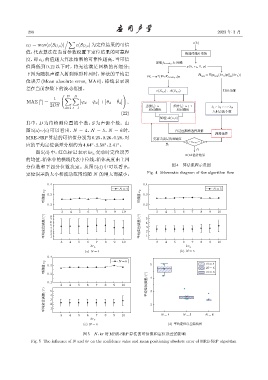
ε U = max(ε(S U,v )) ε(S U,v ) 为定位结果的可信
值，代表算法在当前参数设置下定位结果的可靠程 ঌᤴϬ᧗Ձԫ૱
度，即 ε U 的值越大算法结果的可靠性越高，当可信
ҫᣒf density ς Ꭺಫ
值降低到 0.12 以下时，将无法满足网格的再细分； p̵k֒ r a֒ θ֒ ϕ↽
下图为随机声源入射到球形阵列时，算法的平均定 R /E♭p ↼kr a↽p H ↼kr a↽♯
T
W i /e ↼P oF density i ↽e nm nm nm
位误差 (Mean absolute error, MAE)，棒线表示误
差在当前参数下的波动范围。
ε↼S u֒v ↽aA↼S u֒v ↽ ྲढ़Ѭᝍ
( D S )
1 ∑ ∑
◦
MAE [ ] = φ d − ˆφ d + θ d − θ d ,

ˆ

2DS ेҒࡏ. u ጺѬࡏ. u⇁
d=1 s=1 λ 1 > λ 2 >SSS >λ N
ᄱࠫ྅ϙ ᄱࠫ྅ϙ
(22) К࠱ܦູ˔஝
྅ࣀ ∆↼u֒v↽
其中，D 为待检测位置的个数；S 为声源个数。由
图 5(a)∼(c) 可以看出，N = 4、N = 5、N = 6 时， ᒭᤠऄᎪಫᤥહѼ૶
Ꭺಫᤥહ
MRE-SRP算法的可信值分别为 0.25、0.26、0.28，对 ఞழेҒࡏ൓঴྅ϙ
u ͉ u max ֓
应的平均定位误差分别约为4.64 、2.58 、2.41 。 ௧
◦
◦
◦
ա
图 5(d) 中，红色标记表示 kr a 变动时定位误差
DOAͥᝠፇ౧
的均值，箱体中的横线代表中位线，箱体高度由上四
分位数和下四分位数决定。从图 5(d) 中可以看出， 图 4 算法流程示意图
定位误差的大小和波动范围均随 N 的增大而减小， Fig. 4 Schematic diagram of the algorithm flow
0.4 0.4
N/ N/
Իηϙ ε U 0.3 Իηϙ ε U 0.3
0.2 0.2
3 4 5 6 7 8 9 10 5 3 4 5 6 7 8 9 10
ࣱکࠀͯឨࣀ/(O) 7 6 5 4 3 2 ࣱکࠀͯឨࣀ/(O) 4 3 2
8

1
3 4 5 6 7 8 9 10 1 3 4 5 6 7 8 9 10
kr a kr a
(a) N=4 (b) N=5
0.4 N/
Իηϙ ε U 0.3 5 N/
N/

N/
0.2
0.1 4
3 4 5 6 7 8 9 10 ࣱکࠀͯឨࣀ/(O) 3
ࣱکࠀͯឨࣀ/(O) 4 3 2 2
5

1
3 4 5 6 7 8 9 10 N/ N/ N/
kr a
(c) N=6 (d) ࣱکࠀͯឨࣀኸጳڏ

图 5 N、kr 对 MRE-SRP 算法的可信值和定位误差的影响
Fig. 5 The influence of N and kr on the confidence value and mean positioning absolute error of MRE-SRP algorithm