Page 172 - 《应用声学》2023年第2期

360 2023 年 3 月

E k ↼t↽⊳10 -6 2 1 R  =20 µm
R =10 µm

0
0 0.2 0.4 0.6 0.8 1.0
t/(10 -4 s)
5
(a) ᯶үᮠဋf=1.61T10 Hz
E k ↼t↽⊳10 -6 2 1 R  =20 µm
R  =10 µm
0
0 0.2 0.4 0.6 0.8 1.0
t/(10 -4 s)
(b) ᯶үᮠဋf=3.34T10 Hz
5
E k ↼t↽⊳10 -6 2 1 R =20 µm
R  =10 µm
0
0 0.2 0.4 0.6 0.8 1.0
t/(10 -4 s)
5
(c) ᯶үᮠဋf=2.475T10 Hz
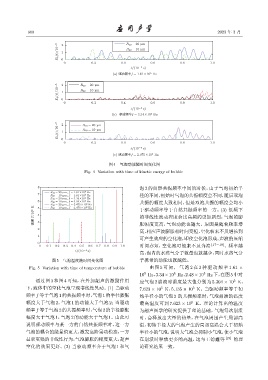
图 4 气泡动能随时间变化图
Fig. 4 Variation with time of kinetic energy of bubble

8 泡 2 的自然共振频率中间的时候，由于气泡初始半
R  =20 µm, f=1.61T10 5 Hz
7 R  =10 µm, f=1.61T10 5 Hz 径的不同，初始时气泡的共振幅度会不同，随后双泡
R =20 µm, f=3.34T10 5 Hz
6 R  =10 µm, f=3.34T10 5 Hz 共振的幅度大致相同，但是双泡共振的幅度会均小
R  =20 µm, f=2.475T10 5 Hz 于驱动频率等于自然共振频率的一方。(3) 低频下
ພए T/10 5 K 4 3 的非线性波动程度会比高频的更加剧烈，气泡的膨
R  =10 µm, f=2.475T10 5 Hz
5

2 胀幅度更高，气泡动能也越大。原因是随着频率增
高，相应声波膨胀相时间变短，空化核来不及增长到
1
可产生效应的空化泡，即使空化泡形成，声波的压缩
0
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 时间亦短，空化泡可能来不及奔溃 [17−18] 。频率越
t/(10 -4 s)
高，泡内的水蒸气分子数量也就越少，同时水蒸气分
图 5 气泡温度随时间变化图 子携带的动能也就越低。
Fig. 5 Variation with time of temperature of bubble 由 图 5 可 知， 气 泡 2 在 3 种 驱 动 频 率 1.61 ×
10 Hz、3.34 × 10 Hz、2.48 × 10 Hz下，在图5中对
5
5
5
通过图 3 和图 4 可知，在外加超声的激励作用 应气泡 2 崩溃时温度最大值分别为 5.304 × 10 K、
5
下，液体中的空化气泡呈现非线性晃动。(1) 当驱动 7.623 × 10 K、5.135 × 10 K。当驱动频率等于初
5
5
频率f 等于气泡1的共振频率时，气泡1的半径膨胀 始半径小的气泡 2 的共振频率时，气泡崩溃的温度
幅度大于气泡 2，气泡 1 的动能大于气泡 2；当驱动 最高温度可到 7.623 × 10 K。理论计算出的温度
5
频率f 等于气泡2的共振频率时，气泡2的半径膨胀 为超声医学的研究提供了理论基础。气泡每次崩溃
幅度大于气泡 1，气泡 2 的动能大于气泡 1。由此可 时，会释放出大量的热量，在气泡周围产生局部高
说明驱动频率与某一方的自然共振频率时，这一方 温，初始半径大的气泡产生的局部高温会大于初始
气泡的耦合的能量值更大，激发高阶晃动模态，一方 半径小的气泡，说明大气泡会抑制小气泡，使小气泡
显示更强的非线性行为，气泡膨胀的幅度更大，超声 在崩溃时释放更多的高温，这与王德鑫等 [19] 的理
空化的效果更好。(2) 当驱动频率介于气泡 1 和气 论研究结果一致。