Page 67 - 《应用声学》2023年第2期

第 42 卷 第 2 期 马雪飞等： 基于高斯混合概率假设滤波的水下目标跟踪算法 255

表 1 仿真参数 GMPHD 算法中新生量测取值为方向取值区间
Table 1 Simulation parameters [0 rad π/3 rad]、时延取值区间 [0.09 s 0.19 s] 各
个区间取中间 2 个 4 等分点，共计 4 种组合，协方差
参数 参数值
2
取值为 diag[0.01 rad 2 0.02 s ]。跟踪效果图如图 3
TS max 40 dB
σ TS 0.089 rad 所示。
f 0 3000 Hz 由于目标均可被直接观测，采用标准差的方式
d 0.25 m
进行分析比较。图 3 中水平方向跟踪误差和竖直方
Z S [−5 m; 0 m]
向跟踪误差如图4和图5所示。
σ Z S ,x ; σ Z S ,y 0.1 m/s; 0.1 m/s
120
Z R1 [0 m; 0 m] JPDAТᐏፇ౧
ࠄᬅᤂүᢾᤜ
σ R 1 ,x ; σ R 1 ,y 0.1 m/s; 0.1 m/s ᧚฾ͯᎶ GMPHDТᐏፇ౧
110
Z R2 [−5 m; 5 m] NNТᐏፇ౧
0.1 m/s; 0.1 m/s
σ R 2 ,x ; σ R 2 ,y 100
T 1 s ቢᄰவՔͯረ/m
仿真实验共分为两部分：第一部分仿真实验是 90
已知运动目标个数下，比较最邻近NN关联算法、高
80
斯假设下最优的 JPDA 关联算法和 GMPHD 滤波
的跟踪效果。第二部分仿真实验是运动目标个数未 70
-100 -90 -80 -70 -60 -50 -40
知下，GMPHD滤波的跟踪仿真分析。 ඵࣱவՔͯረ/m
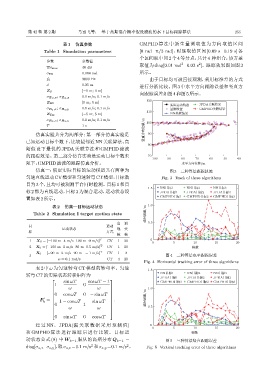
仿真一：假定实际目标的运动模型共有两种为 图 3 三种算法跟踪轨迹
匀速直线运动CV模型和匀速转弯CT模型，目标数 Fig. 3 Track of three algorithms
目为3个，且均可被观测平台同时检测。目标1 和目
1.5 NNᄬಖ1 NNᄬಖ2 NNᄬಖ3
标2 都为直线运动，目标 3 为混合运动，运动状态设 JPDAᄬಖ1 JPDAᄬಖ2 JPDAᄬಖ3
GMPHDᄬಖ1 GMPHDᄬಖ2 GMPHDᄬಖ3
置如表2所示。
表 2 仿真一目标运动状态 1.0
ፐࠫឨࣀ/m
Table 2 Simulation I target motion state
出 消 0.5
目 运动
运动状态 现 失
标 方式
帧 帧
1 X 0 = [−100 m 4 m/s 100 m 0 m/s] T CV 1 20 0
0 5 10 15 20
2 X 0 = [−100 m 2 m/s 80 m 0.5 m/s] T CV 1 20 ࣝ஝
X 0 = [−90 m 2 m/s 90 m − 1 m/s] T CV 1 3
3 图 4 三种算法水平跟踪误差
ω = 0.1 rad/s CT 4 20
Fig. 4 Horizontal tracking error of three algorithms
表 2 中 ω 为匀速转弯 CT 模型的转弯率。匀速
1.5
转弯CT的实际状态转移矩阵为 NNᄬಖ1 NNᄬಖ2 NNᄬಖ3
JPDAᄬಖ1 JPDAᄬಖ2 JPDAᄬಖ3
 
sin ωT cos ωT − 1 GMPHDᄬಖ1 GMPHDᄬಖ2 GMPHDᄬಖ3
1 0
 ω ω  1.0
 
0 cos ωT 0 − sin ωT
 
  ፐࠫឨࣀ/m
′
F =   .
k  1 − cos ωT sin ωT 
0 1  0.5
 ω ω 
 
0 sin ωT 0 cos ωT
经 过 NN、 JPDA(漏 关 联 数 据 采 用 预 测 值) 0
0 5 10 15 20
和 GMPHD 算法进行跟踪后进行比较。目标运 ࣝ஝
动状态公式 (8) 中 W k−1 服从的高斯分布 Q k−1 = 图 5 三种算法竖直跟踪误差
2
diag[σ a,x σ a,y ]，取σ a,x =0.1 m/s 和σ a,y =0.1 m/s 。 Fig. 5 Vertical tracking error of three algorithms
2