Page 40 - 《应用声学》2023年第3期

478 2023 年 5 月

值模拟方法。以充气 (气泡) 和液态球体为例，分别
利用球形目标的解析模型和 FEM/BEM 模型计算
其TS。球体半径假设为 10 mm，充气球体和液态球
体的密度比和声速比见表1。TS随频率变化的计算
结果如图1所示。图1显示，FEM/BEM模型计算结 (a) ࡋ௚ᝈ༥᱓ನֶ

果与解析解高度吻合，充气球体的 TS 远大于液态
球体。

0

ᝍౢവی
(b) XАྟ, Яᦊᳬᓤӝ۫˞᱓᲏
-20 FEM-BEM
-40
TS/dB -60 Ѝඡုʹ Gas-filled sphere

-80 (c) ᤃͫڀᣁ೹ုʹവی
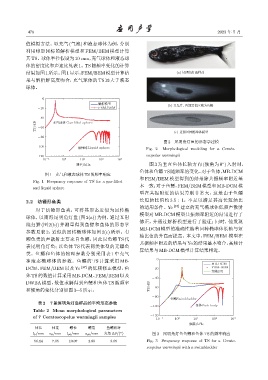
图 2 尾明角灯鱼的形态学建模
-100 ๯ʹု Liquid sphere Fig. 2 Morphological modeling for a Cerato-

-120 scopelus warmingii
10 -1 10 0 10 1 10 2 10 3
◦
ᮠဋ/kHz 图 3 为垂直鱼体长轴方向 (倾角为 0 ) 入射时，
鱼体和鱼鳔TS随频率的变化。对于鱼体，MB-DCM
图 1 充气和液态球体 TS 的频率响应
和 FEM/BEM 模型得到的结果除共振频率附近基
Fig. 1 Frequency response of TS for a gas-filled
本一致；对于鱼鳔，FEM/BEM模型和 MB-DCM 模
and liquid sphere
型在共振附近的结果差别非常大，这是由于鱼鳔
2.2 纺锤形鱼类 长短轴比值约 3.5 : 1，不足以满足其高长短轴比
的适用条件。Ye [37] 建立的充气椭球体低频声散射
对于纺锤形鱼类，可将其形态近似为回转椭
模型对 MB-DCM 模型共振频率附近的结果进行了
球体，以南海尾明角灯鱼 (图 2(a)) 为例，通过 X 射
修正，并通过解析模型进行了验证；同时，他发现
线扫描 (图 2(b)) 并测量得到鱼鳔和鱼体的形态学
MB-DCM 模型的准确性随着回转椭球体长轴与短
参数见表 2，近似的回转椭球体如图 2(c) 所示。有
轴比值的升高而提高。本文中，FEM/BEM 模型在
鳔鱼类的声散射主要来自鱼鳔，因此以鱼鳔 TS 代
共振频率附近的结果与Ye的结果基本吻合，高频计
表尾明角灯鱼；以鱼体 TS 代表同类体型的无鳔鱼
算结果与MB-DCM模型计算结果相近。
类。鱼鳔和鱼体的物理参数分别采用表 1 中充气
和液态椭球体的参数。鱼鳔的 TS 计算采用 MB- 0
MB-DCM
DCM、FEM/BEM 以及 Ye [37] 的低频修正模型，鱼 -20 FEM-BEM
஡࿹[37]
体TS 的数值计算采用 MB-DCM、FEM/BEM 以及
-40
DWBA 模型，数值求解得到鱼鳔和鱼体 TS 随频率
和倾角的变化分别如图3∼5所示。 TS/dB -60
-80
᱓᲏Swimbladder
表 2 7 条尾明角灯鱼样品的平均形态参数
-100 ᱓ʹFish body
Table 2 Mean morphological parameters
of 7 Ceratoscopelus warmingii samples -120
10 -1 10 0 10 1 10 2 10 3
ᮠဋ/kHz
体长 体宽 鳔长 鳔宽 鱼鳔相对
l b /mm a b /mm l sb /mm a sb /mm 夹角 ∆θ/( ) 图 3 尾明角灯鱼鱼鳔和鱼体 TS 的频率响应
◦
56.14 7.05 10.07 2.89 3.09 Fig. 3 Frequency response of TS for a Cerato-
scopelus warmingii with a swimbladder