Page 41 - 《应用声学》2023年第3期

第 42 卷 第 3 期 于小涛等： 有限元/边界元耦合方法在海洋生物目标强度特性研究的应用 479

图4为38 kHz和120 kHz频率入射下，鱼鳔TS 和 DWBA 模型数值求解得到 TS 随频率和倾角的
随鱼类游泳倾角的变化。结果显示，FEM/BEM 变化分别如图 7 和图 8 所示。图7 表明，FEM/BEM
和 MB-DCM 模型的计算结果差别非常大，FEM/ 模型得到的垂直入射时TS频率响应曲线与DWBA
BEM 模型计算的 TS 从垂直入射 (倾角为 0 ) 向两 模型计算结果比较一致，在曲线峰值和谷值处两者
◦
端入射随倾角的增加 TS 减小的速度更慢，且曲线 的结果有所差异。图 8 表明，FEM/BEM 模型得到
相对平滑，没有峰值和谷值的震荡起伏。图 5 为 的 TS 随倾角的变化曲线与 DWBA 模型计算结果
38 kHz和120 kHz入射频率下，鱼体TS随倾角的变 整体比较吻合，但随着倾角增加，两者计算结果的差
化。由图5可知，在垂直入射方向附近，FEM/BEM、 异逐渐增加，尤其曲线峰值和谷值处。
DWBA 和 MB-DCM 模型的计算结果一致，但随
着倾角的变化，3 种模型计算结果的差异逐渐增 -50
-60 MB-DCM
加；FEM/BEM 和 MB-DCM 模型吻合的倾角范围 DWBA
-70 FEM-BEM
极窄，FEM/BEM 模型和 DWBA 模型吻合的倾角 -80
TS/dB -100
范围较宽。 -90
-30
-110
-40 MB-DCM -120
FEM-BEM
-50 -130
-60 -140 -90 -70 -50 -30 -10 10 30 50 70 90
TS/dB -70 Ϛᝈ/(O)

-80 (a) 38 kHz
-90 -50
MB-DCM
-60
-100 DWBA
-70 FEM-BEM
-110
-90 -70 -50 -30 -10 10 30 50 70 90 -80
TS/dB -90
Ϛᝈ/(O)
(a) 38 kHz
-30 -100
-110
-40 MB-DCM
FEM-BEM -120
-50
-130
TS/dB -60 -140 -90 -70 -50 -30 -10 10 30 50 70 90
-70
Ϛᝈ/(O)
-80 (b) 120 kHz
-90
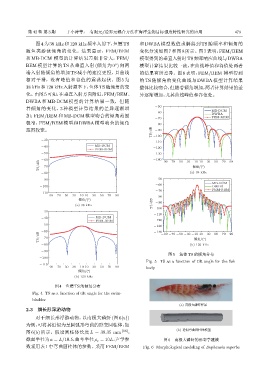
图 5 鱼体 TS 的倾角分布
-100
Fig. 5 TS as a function of tilt angle for the fish
-110
-90 -70 -50 -30 -10 10 30 50 70 90 body
Ϛᝈ/(O)
(b) 120 kHz

图 4 鱼鳔 TS 的倾角分布
Fig. 4 TS as a function of tilt angle for the swim-
bladder
(a) ӯౝܸᇠᙋನֶ
2.3 细长形浮游动物
对于细长形浮游动物，以南极大磷虾 (图 6(a))
为例，可将其近似为呈圆弧形弯曲的形变圆柱体，如
图 6(b) 所示。假设圆柱体长度 L = 38.35 mm [36] ， (b) ᤃͫिజړಏʹവی
截面半径为a = L/10.5，曲率半径ρ c = 10L，声学参 图 6 南极大磷虾的形态学建模
数采用表 1 中弯曲圆柱体的参数。采用FEM/BEM Fig. 6 Morphological modeling of Euphausia superba