Page 108 - 《应用声学》2023年第4期

770 2023 年 7 月

说明沉积层简正波到达时间差对这两个参数比较 3 实验数据分析
敏感，将沉积层简正波到达时间差作为代价函数反
演得到这两个参数的可信度比较高；沉积层密度和 3.1 沉积层简正波频散曲线提取
基底声速的敏感性虽然要低于沉积层厚度和沉积
实验于 2018 年 5 月在南中国海北部大陆坡海
层声速，但仍然不可忽略；而基底密度、海深和距离
域开展，期间在海底放置了接收水听器，深度约为
这 3 个参数的敏感性曲线比较平缓，没有明显的峰
1740 m，并投掷了一些沉底弹。选择距离水听器约
值，说明这 3 个参数对沉积层简正波到达时间差不
8.46 km 的沉底弹进行分析，该沉底弹与水听器之
敏感，因而反演得到的这3个参数可信度不高。
间的海底地形相对比较平坦。图3 所示模型中的水
根据图 5 所示的环境参数敏感性结果，结合
层声速剖面为实验期间水听器所在站点实测的声
Cao 等 [13] 的研究，可以发现海深和水层声速剖面
速剖面，其中声道轴深度在 1130 m，声道轴声速为
不均匀性对沉积层第一阶简正波的群速度基本
1483.5 m/s，底部海水声速为 1488.6 m/s，海表面声
没有影响，而海底沉积层相对水层声速比值和沉
速为1537.1 m/s，为典型的不完全深海声道。
积层厚度对沉积层简正波群速度的影响非常显
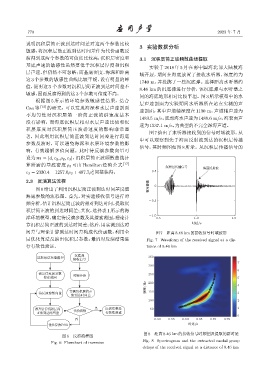
图 7 给出了水听器接收到的信号时域波形，从
著，因此利用沉积层简正波到达时间差进行海底
中可以观察到先于海面反射波到达的沉积层传播
参数反演时，可以避免海深和水层环境参数的影
信号，其时频图如图 8 所示。从沉积层传播信号的
响，有效缓解多值问题。此时待反演参数向量可
设为 m = [d, c 2 , ρ 2 , c 3 ]，沉积层简正波频散曲线计
算所需的基底密度 ρ 3 可由 Hamilton 经验公式 [17] ොሥࡏ͜୧ηՂ ๒᭧Ԧ࠱ฉ
c 3 = 2330.4 − 1257.0ρ 3 + 487.7ρ 间接获得。 0.5
2
3
2.3 反演算法流程
图6 给出了利用沉积层简正波到达时间差反演 ᄱࠫࣨϙ 0
海底参数的流程图。首先，对实验接收信号进行时
-0.5
频分析，估计沉积层简正波的相对到达时间，提取沉
积层简正波的到达时间差；其次，选择表1 所示的海
-1.0
洋环境模型，确定待反演参数及其搜索范围，理论计 0.5 1.0 1.5
算沉积层简正波的到达时间差；然后，用实测到达时 ௑ण/s
间差与理论计算到达时间差构成代价函数，利用全 图 7 距离 8.46 km 的接收信号时域波形
局优化算法反演出沉积层参数；最后对反演结果进 Fig. 7 Waveform of the received signal at a dis-
行有效性验证。 tance of 8.46 km
ොअु
ᤥԩ๒ภဗܒവی 350
ଌஆηՂ
7
300
6
ᆸࠀॠԦ໦Ԡ஝ ௑ᮠѬౢ 250
ଽጊᔵڊ 5
ᮠဋ/Hz 200 4
ࠄ฾ොሥࡏእ൤ 150
ॠԦ໦Ԡ஝Ք᧚ 3
ฉ҂᣺௑ᫎࣀ
100 2
വیᝠካොሥࡏእ ͉̽Ѧ஝ ௧ Ԧ໦ፇ౧ԣ 50 1
൤ฉ҂᣺௑ᫎࣀ ద஍ভᰎ᝽
0
ա 0.50 0.55 0.60 0.65 0.70 0.75
͖ӑካขPSO ௑ण/s
图 8 距离 8.46 km 的接收信号时频图及提取的群时延
图 6 反演流程图
Fig. 8 Spectrogram and the extracted modal group
Fig. 6 Flowchart of inversion
delays of the received signal at a distance of 8.46 km