Page 87 - 《应用声学）》2023年第5期

第 42 卷 第 5 期 杨丽荣等： 基于局部线性嵌入的特征融合方法在岩石破裂状态分类的应用 979

影响，本文采用极大似然估计法确定砂岩破裂各
0.20 100
状态特征数据集的低维子空间维数 d。通过构建近
0.16
邻间距离的似然函数，可得到全局数据结构的低维
ྲढ़ϙܸ࠵ 0.12 50 ግሥ᠈࿹ဋ 特征。 0.2

0.08
ኄʷ᫽඀
ኄ̄᫽඀
0.1 ኄʼ᫽඀
0.04
ኄپ᫽඀
PCA2
0 0 0
0 1 2 3 4 5 6 7 8
Ғ7˔ྲढ़ϙ
-0.1
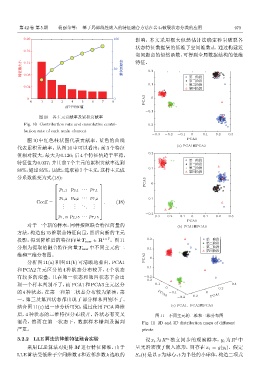
图 10 各主元贡献率及累积贡献率
Fig. 10 Contribution rate and cumulative contri- -0.2
bution rate of each main element
-0.3 -0.2 -0.1 0 0.1 0.2 0.3
图 10 中红色柱状图代表贡献率，蓝色的曲线 PCA1
代表累积贡献率。从图 10 中可以看出：前 3 个特征 (a) PCA1֗PCA2
值相对较大，最大为 0.126；后 4 个特征值趋于平稳， 0.2
特征值为 0.037；并且前 7 个主元的累积贡献率达到 ኄʷ᫽඀
ኄ̄᫽඀
88%，超过 85%。因此，选取前 7个主元，这样主元成 0.1 ኄʼ᫽඀
ኄپ᫽඀
分系数就变为式(18)：
PCA3
  0
p 1,1 p 2,1 · · · p 7,1
 
 
 p 1,2 p 2,2 · · · p 7,2  -0.1
Coeff =  . . . .  . (18)
 . . . . . 
 . . . 
 
-0.2
p 1,15 p 2,15 · · · p 7,15 -0.3 -0.2 -0.1 0 0.1 0.2 0.3
PCA1
对于一个新的样本，同样按照联合特征向量的 (b) PCA1֗PCA3
方法，构造出 15 维联合特征向量，然后向新的主元
投影，得到降维后的特征向量 T new ∈ R 1×7 。图 11 0.2 ኄʷ᫽඀
ኄ̄᫽඀
分别为提取的融合特征向量 T new 中不同主元的二 0.1 ኄʼ᫽඀
ኄپ᫽඀
维和三维分布图。 PCA3 0
分析图 11(a) 和图 11(b) 可清晰地看出，PCA1
-0.1
和 PCA2 主元区分的 4 种状态分布较开，4 个状态
有较多的混叠，且在第一状态和第四状态下会出 -0.2
0.2
现一个样本判别不了，而 PCA1 和 PCA3 主元区分 0.1 0.4
0 0.2
的 4 种状态，在第一和第二状态分布较为紧凑，第 PCA2 -0.1 0
-0.2 -0.2 PCA1
一、第三及第四状态都出现了部分样本判别不了。
结合图 11(c) 进一步分析可知，通过使用 PCA 降维 (c) PCA1njPCA2֗PCA3
后，4 种状态的三维特征分布较开，各状态有交叉 图 11 不同主元的二维和三维分布图
混叠，然而在第一状态下，数据样本错判及漏判 Fig. 11 2D and 3D distribution maps of different
严重。 pivots

3.2.2 LLE算法的降维特征融合实验 设 x i 为 R 独立同步的观察样本，y i 为 R 中
d
m
采用 LLE 算法对矩阵 M 进行特征降维，由于 呈光滑密度 f 嵌入流形，则存在 x i = g(y i )。假定
LLE 算法受低维子空间维数 d和近邻参数 k 选取的 S x (t) 是以x 为球心、t 为半径的小球体，构造二项式