Page 88 - 《应用声学）》2023年第5期

980 2023 年 9 月

非其次过程，即 0.84、0.8。因此确定近邻参数 k = 5，此时 LLE 算法
n 降维后融合特征的聚类效果如图13所示。
∑
N(t, x) = I {x i ∈ S x (r)}, (19)
i=1 0.9
式 (19) 中，I {x i ∈ S x (r)} 为示性函数，用泊松分布 0.8
近似该过程可得 0.7

ኄ̄᫽඀
λ(t) = f(x)V (d)dt d−1 , (20) 0.6 ኄʷ᫽඀
ኄʼ᫽඀
គѿဋ 0.5 ኄپ᫽඀
式 (20) 中，V (d) 为 d 维空间下球的体积函数。令 0.4
θ = lg(f(x))，则N(t)的似然函数可表示为 0.3
r r
∫ ∫ 0.2
L(d, θ) = lg λ(t)dN(t) − λ(t)dt. (21)
0.1
0 0
0
0 2 4 6 8 10 12 14 16 18 20
∂l ∂l ᥶۫Ԡ஝K
在两个约束条件 = 0 和 = 0下，d r (x)可
∂θ ∂d
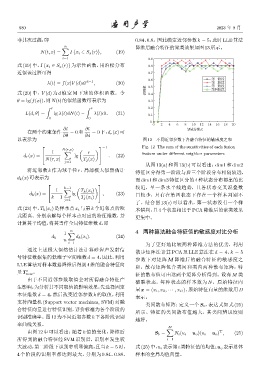
以表示为 图 12 不同近邻参数下各融合特征的敏感度之和
  −1 Fig. 12 The sum of the sensitivities of each fusion
N(r,x) ( )
1 ∑ r feature under different neighbor parameters
d r (x) =  lg  . (22)
N(r, x) T j (x)
j=1
从图 13(a) 和图 13(b) 可以看出：dim1 和 dim2
将近邻数 k 作为球半径 r，局部极大似然估计
特征区分得第一阶段与后三个阶段分布相隔较远，
d k (x)可表示为
而 dim1 和 dim3 特征区分的 4 种状态分布都靠的比
 
k−1 ( ) 较近，呈一条水平线趋势，且各状态交叉混叠数
1 ∑ T k (x i )
d k (x) =  lg  , (23) 目较少，只有在第四状态下存在一个样本判别不
k − 1 T j (x i )
j=1
了。结合图 13(c) 可以看出，第一状态没有一个样
式 (23) 中，T k (x i ) 是样本点 x i 与第 k 个近邻点的欧 本错判，且 4 个状态相比于 PCA降维后的聚类效果
式距离。分别求解每个样本点对应的特征维数，并 更集中。
计算其平均值，将其当作全局特征维数d，即
n 4 两种算法融合特征值的敏感度对比分析
1 ∑
d k = d k (x i ). (24)
n
i=1
为了更好地比较两种降维方法的优劣，利用
通过上述极大似然估计法计算砂岩声发射信
散步矩阵法计算 PCA 及 LLE 算法在 d = 4、k = 5
号特征数据集的低维子空间维数 d = 4，因此，利用
参数下对矩阵 M 降维后的融合特征的敏感度之
LLE算法对样本数据降维后得到4维的融合特征向
和。散布矩阵包含类间和类内两种散布矩阵，特
′
量T new 。 征的散布值可由这两个矩阵分析得到。设有 M 类
由于不同近邻参数取值会对所得融合特征产
破裂状态，每种状态的样本数为 N。原始特征向
生影响，为分析其不同取值的影响效果，先选择固定
量 x = (x 1 , x 2 , · · · , x D )，原始特征向量的维数用 D
本征维数 d = 4，然后改变近邻参数 k 的取值，利用
表示。
支持向量机 (Support vector machines, SVM) 对融
类间散布矩阵：定义一个 S b ，表达式如式 (25)
合特征向量进行特征识别，评价标准为各个阶段的
所示。特征的类间散布值越大，其类间辨识度则
识别准确率。图12为不同近邻参数k 下各阶段识别
越好。
率曲线关系。
M
由图 12 中可以看出：随着 k 值的变化，降维后 S b = ∑ N i (u i − u o )(u i − u o ) , (25)
T
所得到的融合特征经 SVM 识别后，识别率发生较 i=1
大波动，第二阶段下识别率明显偏高，且当k = 5时， 式(25)中，u i 表示第i类特征值的均值；u o 表示总体
4 个阶段的识别率都达到最大，分别为 0.84、0.88、 样本的全局均值向量。