Page 83 - 《应用声学）》2023年第5期

第 42 卷 第 5 期 杨丽荣等： 基于局部线性嵌入的特征融合方法在岩石破裂状态分类的应用 975

由图 4(a) 可以看出，R10 岩样在应力前期，应 曲线斜率逐渐减小到零。失稳破坏阶段(CD)：岩体
变变化率减小，岩石内部相对变形率在应力达到 强度大大降低，宏观破裂基本形成，但破裂面存在一
12.1 MPa时逐渐保持不变，试件被破坏产生大量新 定摩擦，且具备一定承载能力。
的微裂纹汇合贯通的应力为 45.7 MPa，轴向应变率
2.4 砂岩声发射信号时域特征提取
增大。
对于时间序列模型，目前存在的主要问题是
从图 4(b) 可知，在预加载时，G15 岩样在未发
仅对平稳过程具有较好的分析效果，对非平稳过
生应变时就有一定的轴应力，此后先向上凹，斜率
程则表现得无能为力。而岩石破裂过程中产生的
由小变大，在应变为 0.0014、斜率为直线时应力为
声发射信号表现为较强的非平稳过程，直接进行
5.9 MPa，试件所能承受的极限为28.2 MPa，破坏后
AR 建模效果不太理想，而经过改进的集合经验模
蠕变过程产生可能是加载应力和加载的持续时间
态分解 (Ensemble empirical mode decomposition,
导致的。
EEMD)正好解决了这一问题。因此本文在建立AR
50
C↼⊲֒⊲↽ 模型之前先采用改进 EEMD 对岩石声发射信号进
45
40 D↼⊲֒⊲↽ 行预处理，将其分解为若干个有效的平稳的本征模
35 B↼⊲֒⊲↽ 态函数 (Intrinsic mode function, IMF) 分量，然后
ऄҧ/MPa 30 对各 IMF 分量采用 AIC 准则函数确定模型的最佳
25
阶次，建立各个 IMF 分量的 AR模型，提取 AR模型
20
的自回归参数构成特征向量。
15
10 A↼⊲֒⊲↽ 采用改进的 EEMD 算法对第一破裂阶段下连
5 续声发射时域波形进行分解，取前 8 个 IMF 波形如
O↼֒↽
0 图5 所示。可以看出，IMF5∼IMF8分量是原始信号
0 0.005 0.010 0.015 0.020 0.025 0.030
ऄԫ 中分解出的时间尺度最长、频率较低的分量，代表
(a) ጚᆋࡸR10
信号中的低频成分。
30
C↼⊲֒⊲↽ 为了更加清晰地了解阈值选取的普遍性，采用
改进的 EEMD 算法分别对 10 组不同岩石破裂状态
25
下声发射信号进行分解，并求取分解出的各分量与
B↼⊲֒⊲↽
ऄҧ/MPa 20 D↼⊲֒⊲↽ 原始信号的云相似值，最后取每组的前 6 个分量的
15
云相似值进行曲线拟合，如图6所示。
10 从图 6 可知，前 3 个分量 (IMF1∼MF3) 的云相
似值都很大。由云模型理论可知，云相似值越大
5 A↼⊲֒⊲↽
则其含有原始信号的信息量越多，与原始信号的
O↼֒↽
0 关联性更强，可以完全反映原始信号的特征。而
0 0.002 0.004 0.006 0.008
ऄԫ IMF4∼IMF6 的值相对较小，说明是与原始信号无
(b) ጚᆋࡸG15
关的噪声。根据多组信号统计分析，将IMF1、IMF2、
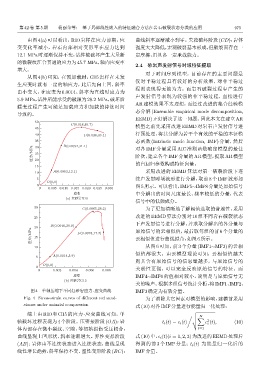
图 4 单轴压缩下不同红砂岩应力 -应变曲线 IMF3确定为有效分量。
Fig. 4 Stress-strain curves of different red sand- 为了消除其它因素对模型的影响，建模前采用
stones under uniaxial compression 式(10)对各IMF分量进行能量归一化处理：
综上由 R10 和 G15 的应力 -应变曲线可知，单 / u
v
N
u∑
轴破坏过程表现为 4 个阶段。压密接阶段 (OA)：岩 ˆ c i (t) = c i (t) t c (t), (10)
2
i
体内部存在微小裂纹、空隙，等初始损伤受压闭合， t=1
曲线呈现上凹形状，斜率逐渐增大。弹性变形阶段 式(10) 中，c i (t)(i = 1, 2, 3) 为改进的 EEMD处理后
(AB)：岩体由不连续状态进入连续状态，曲线呈现 得到的前 3 个 IMF 分量；ˆc i (t) 为能量归一化后的
线性增长趋势，斜率保持不变。塑性变形阶段(BC)： IMF分量。