Page 85 - 《应用声学）》2023年第5期

第 42 卷 第 5 期 杨丽荣等： 基于局部线性嵌入的特征融合方法在岩石破裂状态分类的应用 977

范围也较宽。在第三破坏阶段下，频带范围最宽，低 后，砂岩声发射信号的双谱特征可以较好地区分岩
频高频都有，且高频信息聚集；在岩样破坏后第四阶 石不同破裂阶段，但最终是得到双谱高阶矩阵，数据
段，应力值逐渐减小，但仍具有声发射现象，但强度 量的维数较大，不适于机器识别，因此应用奇异值分
较弱，高频信号消失，频率主要又转向低频聚集。 解理论对高阶矩阵进行处理，提取出多个奇异值作
也可直观地看出，信号经去均值及归一化处理 为最具代表性的特征向量，以便进行智能识别。

P=9.52 MPa P=12.84 MPa
0.4 0.4
0.3 0.3
0.2 0.2
f  /(10 5 Hz) -0.1 0 f  /(10 5 Hz) -0.1 0
0.1
0.1

-0.2 -0.2
-0.3 -0.3
-0.4 -0.4
-0.5 -0.5
-0.5 -0.4 -0.3 -0.2 -0.1 0 0.1 0.2 0.3 0.4 -0.5-0.4-0.3-0.2-0.1 0 0.1 0.2 0.3 0.4
5
5
f  /(10 Hz) f  /(10 Hz)
(a) ኄʷᆡᜈ᫽඀ (b) ኄ̄ᆡᜈ᫽඀
P=31.87 MPa P=28.25 MPa
0.4 0.4
0.3 0.3
0.2 0.2
0.1
0.1
f  /(10 5 Hz) -0.1 0 f  /(10 5 Hz) -0.1 0

-0.2 -0.2
-0.3 -0.3
-0.4 -0.4
-0.5 -0.5
-0.5 -0.4 -0.3 -0.2 -0.1 0 0.1 0.2 0.3 0.4 -0.5 -0.4 -0.3 -0.2 -0.1 0 0.1 0.2 0.3 0.4
5
5
f  /(10 Hz) f  /(10 Hz)
(c) ኄʼᆡᜈ᫽඀ (d) ኄپᆡᜈ᫽඀
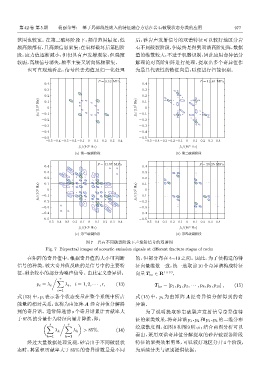
图 7 岩石不同破裂阶段下声发射信号的双谱图
Fig. 7 Bispectral images of acoustic emission signals at different fracture stages of rocks

在矩阵的奇异值中，根据奇异值的大小可判断 的，但都分布在 4∼10 之间。因此，为了使构造的特
信号的种类，较大奇异值反映的是信号中的主要特 征向量维数一致，统一选取前 10个奇异谱构成特征
征，剩余较小的部分为噪声信号。由此定义奇异谱： 向量T ho ∈ R 1×10 ，
/ r
∑
λ i , i = 1, 2, · · · , r, (13)
p i = λ i T ho = [p 1 , p 2 , p 3 , · · · , p 8 , p 9 , p 10 ] , (15)
i=1
式 (13) 中，p i 表示各个状态变量在整个系统中所占 式 (15) 中，p i 为由矩阵 A 经奇异值分解得到的奇
能量的相对关系，也称为由矩阵A 经奇异值分解得 异谱。
到的奇异谱。通常筛选前 s 个奇异谱累计贡献率大 为了说明提取砂岩破裂声发射信号奇异值特
于85%的分量作为特征向量并降维，即： 征的聚类效果，将奇异谱p 1 、p 2 和p 1 、p 3 的二维分布
( s / r )
∑ ∑ 绘成散度图，如图 8 和图 9 所示；结合两图分析可以
λ k λ k > 85%. (14)
看出，采用双谱奇异值分解提取的砂岩破裂各阶段
k=1 k=1
经过大量数据处理发现，砂岩出于不同破裂状 特征的聚类效果明显，可以较好地区分开 4 个阶段，
态时，其累积贡献率大于 85% 的奇异谱数量是不同 为后续分类与识别提供依据。