Page 21 - 《应用声学》2023年第6期

第 42 卷 第 6 期 安秉文等： 光纤声传感反正切解调的采样率与信号幅度关系 1131

20 1
ࣨए 0
10
ࣨए/rad 0 -1 -1 0 1

-10 ௑ᫎ/s
(c) ኄʷ᡹ᣥѣηՂ V 
-20
1
-1 0 1
௑ᫎ/s ࣨए 0
(a) ᣥКηՂ
2 -1
-1 0 1
௑ᫎ/s
1
(d) ኄ̄᡹ᣥѣηՂ V 
ࣨए/rad 0 1

ࣨए 0
-1
-1
-2
-1 0 1 -1 0 1
௑ᫎ/s ௑ᫎ/s
(b) Ԧ൤ѭᝍូηՂ (e) ኄʼ᡹ᣥѣηՂ V 

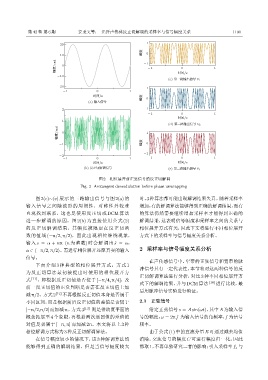
图 2 相位展开前正弦信号的反正切解调
Fig. 2 Arctangent demodulation before phase unwrapping

图 2(c)∼(e) 展示的三路输出信号与图 2(a) 的 时，3种算法都可能出现解调结果失真。随着采样率
输入信号之间除波形的周期性、对称性外较难 增加，有的解调算法能够得到正确的解调结果，而有
直观找到联系，这也是使用反正切或 DCM 算法 的算法仍然需要继续增加采样率才能得到正确的
进一步解调的原因。图 2(b) 为直接使用公式 (2) 解调结果，这表明信号幅度和采样率之间的关系与
的反正切解调结果，其幅度被限定在反正切函 相位展开方式有关，因此下文将进行不同相位展开
数的值域 (−π/2, π/2)，因此出现相位缠绕现象， 方式下的采样率与信号幅度关系分析。

输入 s = α + nπ (n 为整数) 时会解调出 ˆs = α，
α ∈ (−π/2, π/2)。需进行相位展开还原真实的输入 2 采样率与信号幅度关系分析
信号。
在声传感信号中，窄带的正弦信号和宽带的脉
下面介绍 3 种典型的相位展开方式。方式 1
冲信号具有一定代表性，本节将对这两种信号的反
为反正切算法最初被提出时使用的相位展开方
正切解调算法进行分析，对比 3 种不同相位展开方
式 [11] ，即根据反正切值是否位于 [−π/4, π/4]，及
式下的解调结果，并与 DCM 算法 [10] 进行比较，最
前一反正切值的正负判断是否需在反正切值上加
后用脉冲信号实验进行验证。
减π/2。方式 2 [12] 不再根据反正切值本身是否属于
不同区间，而是根据前后反正切值的差值是否属于 2.1 正弦信号
[−π/2,π/2]而加减π。方式3 [13] 则是借助复平面的 给定正弦信号 s = A sin(ωt)，其中 A 为输入信
概念拓展至 4 个象限，再根据两次返回值的差值绝 号的幅度，ω = 2πf 为输入信号的角频率，f 为信号
对值是否属于 [−π, π] 而加减 2π。本文将以上 3 种 频率。
相位解调方式称为3种反正切解调算法。 由于公式 (1) 中的直流分量 B 可通过减去均值
在信号幅度较小的情况下，这 3 种解调算法均 消除，交流信号的幅度 C 可进行幅度归一化，因此
能够得到正确的解调结果。但是当信号幅度较大 都取1，不再单独研究二者的影响；引入采样率f s 与