Page 22 - 《应用声学》2023年第6期

1132 2023 年 11 月

信号频率 f 的比值 K j = f s /f 表示一周期内采样的 DCM 算法使用的相对采样率 K DCM = 160 与 K 1
点数，并记为相对采样率，下标 j = 1, 2, 3 表示第 j 接近。计算时发现 3 种反正切解调方式的误差均在
种反正切解调方式。在接下来的分析中不失一般性 3.55 × 10 −15 ，而即使K DCM = 2000 时，其最大误差
地取f = 1。输入信号仍用图2(a)所示的信号。 为 0.003 > 0.01% × A = 0.002。这是因为 DCM 算
记相位展开后的解调结果为 ˆs，以 法的求导、积分等步骤建立在微元假设上，因此误
差较大，而反正切算法则不是。在计算时间上3种反
|s − ˆs| max < 0.01% × A (4) −4
正切解调方式均在10 s量级，DCM算法为0.11 s，
为误差判据，用于分析解调结果的失真度。计算了 表明DCM在实时性上的不足。
在采样率刚刚满足误差判据时 3 种反正切解调方 为进一步探究采样率与信号幅度之间的关系，
式及 DCM 算法的解调结果与输入信号间的误差， 计算了信号幅度 A ∈ [1, 1000] 时 3 种反正切解调方
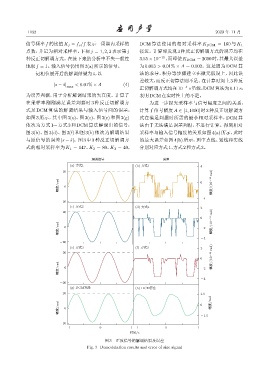
如图 3 所示，其中图 3(a)、图 3(c)、图 3(e) 和图 3(g) 式在满足判据时所需的最小相对采样率，DCM 算
依次为方式 1∼ 方式 3 和 DCM 算法解调出的信号， 法由于无法满足误差判据，不进行计算。得到相对
图 3(b)、图 3(d)、图 3(f) 和图 3(h) 依次为解调结果 采样率与输入信号幅度的关系如图 4(a) 所示，此时
与原信号的误差 |s − ˆs|。图 3 中 3 种反正切解调方 的最大误差如图 4(b) 所示，图中点线、划线和实线
式的相对采样率为 K 1 = 147、K 2 = 80、K 3 = 40， 分别对应方式1、方式2和方式3。

ᝍូηՂ ឨࣀ
(a) வर1 (b) வर1 4
20

ࣨए/rad 0 0 ࣨए/(10 -15 rad)

-4
-20
(c) வर2 (d) வर2 2
20
0 ࣨए/(10 -15 rad)
ࣨए/rad 0 -2

-4
-20
(e) வर3 (f) வर3 2
20
0 ࣨए/(10 -15 rad)
ࣨए/rad 0 -2

-4
-20
(g) DCMካข (h) DCMካข
20 1.5
ࣨए/rad 0 0 ࣨए/rad

-1.5
-20
-1 0 1 -1 0 1
௑ᫎ/s
图 3 正弦信号的解调结果及误差
Fig. 3 Demodulation results and error of sine signal