Page 23 - 《应用声学》2023年第6期

第 42 卷 第 6 期 安秉文等： 光纤声传感反正切解调的采样率与信号幅度关系 1133

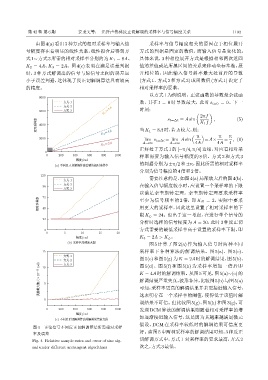
由图4(a)看出3种方式的相对采样率与输入信 采样率与信号幅度相关的原因在于相位展开
号幅度存在着明显的线性关系，线性拟合后得到方 方式的判据是固定的数值，而输入信号是变化的。
式1∼ 方式 3 所需的相对采样率分别约为 K 1 = 8A、 具体来说，3 种相位展开方式是根据相邻两次返回
K 2 = 4A、K 3 = 2A。图 4(c) 表明在满足误差判据 值的差值或是所属区间的关系来移动坐标基准、展
时，3 种方式解调出的信号与原信号之间的误差远 开相位的，因此输入信号斜率最大处前后的导数
小于误差判据，这体现了反正切解调算法具有较高 (方式 1、方式 2 和方式 3) 或函数值 (方式 1) 决定了
的精度。 相对采样率的要求。
以方式 1 为例说明。正弦函数的导数是余弦函
8000
வर 1 数，其在 t = 0 时导数最大，此时 s t=0 = 0。下一
வर 2
6000 வर 3 K aA 时刻： ( )
2πf , (5)
s t=∆t = A sin
ᄱࠫ᧔ನဋ 4000 当K 1 = 8A时，若A较大，则： K 1 f

π
2000 K  aA lim s t=∆t = lim A sin ( π ) =A× π = , (6)
K aA A→∞ A→∞ 4A 4A 4
正好处于方式 1 的 [−π/4, π/4] 边缘，对应着相对采
0
0 200 400 600 800 1000 样率需要为输入信号幅度的 8 倍。方式 2 和方式 3
ࣨए/rad
的判据分别为 ±π/2和±π，因此所需的相对采样率
(a) ˀՏԦ൤ѭᝍូካขᭊ᜶ᄊᄱࠫ᧔ನဋ
分别为信号幅度的4倍和2倍。
120
வर 1 需要注意的是，如图4(a)局部放大后的图4(b)，
வर 2
96 在输入信号幅度较小时，应设置一个采样率的下限
வर 3
以满足奈奎斯特定理。奈奎斯特定理要求采样率
72
ᄱࠫ᧔ನဋ 48 至少为信号频率的 2 倍，即 K N = 2，实际中要采
用更大的采样率，因此这里设置了相对采样率的下
限 K L = 24。也出于这一考虑，在进行单个信号的
24
分析时选择的信号幅度为 A = 20，此时 3 种反正切
0 方式需要的最低采样率高于设置的采样率下限，即
0 5 10 15 20
ࣨए/rad K 3 = 2A > K L 。
(b) ᧔ನဋࡍᦊஊܸڏ
图 5 计算了图 2(a) 作为输入信号时两种不同
15 采样率下各种算法的解调结果。图 5(a)、图 5(c)、
வर 1
வर 2 图 5(e) 和图 5(g) 为 K = 2A 时的解调结果，图5(b)、
ឨࣀతܸϙ/(f10 -12 rad) 5 K = 4A时的解调结果。从图5 可见，图5(a)∼(c)的
வर 3
图 5(d)、图 5(f) 和图 5(h) 为采样率增加一倍后即
10
解调结果严重失真，波形各异，比较图5(b)与图5(a)
可知，采样率更高的解调结果并未更接近输入信号，

0 这表明存在一个采样率的阈值，使得低于该值时解
调结果不可信。但比较图5(g)、图5(h)和图 3(g)，可
0 200 400 600 800 1000 发现 DCM 算法的解调结果则随着相对采样率的增
ࣨए/rad
加逐渐接近输入信号，这是因为其越来越满足微元
(c) ˀՏԦ൤ѭᝍូካขᄊᝍូឨࣀతܸϙ
假设，DCM 在采样率较低时的解调结果可信度更
图 4 正弦信号不同反正切解调算法所需相对采样
率及误差 好。由图 5 中两种采样率的解调结果可知，3 种反正
Fig. 4 Relative sample rates and error of sine sig- 切解调方式中，方式 1 对采样率的要求最高，方式 2
nal under different arctangent algorithms 次之，方式3最低。