Page 33 - 《应用声学》2023年第6期

第 42 卷 第 6 期 王晨青等： 压电陶瓷非线性对大功率换能器结构参数匹配影响的计算分析 1143

若将式 (8) 中的非线性项去掉，再通过相同方 能器频响曲线峰值由谐振峰变为向低频偏移谐振
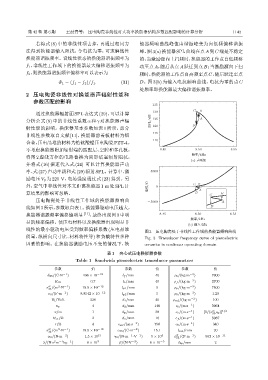
法得到换能器输入阻抗，令电抗为零，可求解线性 峰。图3(a)换能器SPL曲线在点A到C 端是不稳定
换能器谐振频率。设线性状态的换能器谐振频率为 的，当激励源向上扫频时，换能器的工作点自低频移
f 1 ，非线性工作域下的换能器最大偏移谐振频率为 动至点A，随后从点A跃迁到点B；当激励源向下扫
f 2 ，则换能器谐振频率偏移率可以表示为 频时，换能器的工作点自高频至点C，随后跃迁至点
Φ 1 = (f 1 − f 2 )/f 1 . (31) D。图 3(b) 为输入电抗频响曲线，电抗为零的点 C
处频率即换能器最大偏移谐振频率。
2 压电陶瓷非线性对换能器声辐射性能和
参数匹配的影响
135
通过换能器辐射面 SPL 表达式 (29)，可以计算 130 C B
分析公式 (8) 中的非线性系数 α 和 γ 对换能器声辐 SPL/dB 125 A
射性能的影响。换能器基本参数如表 1 所示，部分 120 D
115
非线性参数取自文献 [11]，换能器前盖板材料为铝
110
合金，压电晶堆的材料为锆钛酸铅压电陶瓷PZT-4。
不考虑换能器附加辐射端的匹配层、空腔和多孔板， 8.45 8.50 8.55
ᮠဋ/kHz
将图 2 虚线方框的电路替换为圆形活塞辐射阻抗，
(a) ܦԍጟ
并将式 (16) 振速代入式 (24) 可以计算换能器声功
率、式(27)声功率级和式(29)辐射SPL。计算中，激 5000
励电压 V 0 为 220 V，电场强度通过式 (23) 得到。另
外，空气中非线性对本文距离换能器 1 m 处 SPL 计 ႃઈ/W 0 C B
算结果的影响可忽略。 D A C B
压电陶瓷处于非线性工作域的换能器频响曲 -5000 A
线如图3所示，参数取自表1。换能器驱动电压越大， D
换能器谐振频率偏移越明显 [11] ，最终出现图 3 中明 8.45 8.50 8.55
ᮠဋ/kHz
显的频率偏移。使压电材料以及换能器出现明显非
(b) ᣥКႃઈ
线性的最小驱动电压受到频率偏移系数 (压电晶堆
图 3 压电陶瓷处于非线性工作域的换能器频响曲线
质量、纵横向尺寸比、材料特性等) 和负载特性多种 Fig. 3 Transducer frequency curve of piezoelectric
因素的影响。在换能器激励电压不变的情况下，换 ceramics in nonlinear operating domain

表 1 夹心式压电换能器参数
Table 1 Sandwich piezoelectric transducer parameters
参数 值 参数 值 参数 值
d 33 /(C·N −1 ) 496 × 10 −12 l f /mm 40 ρ b /(kg·m −3 ) 7800
0.7 l b /mm 40 ρ f /(kg·m −3 ) 2700
K 33
2
E
s /(m ·N −1 ) 15.5 × 10 −12 l p1 /mm 5 ρ p/(kg·m −3 ) 7500
33
ε 0 /(F·m −1 ) 8.8542 × 10 −12 l p2 /mm 5 ρ 0 /(kg·m −3 ) 1.29
V 0 /Volt 220 d 1 /mm 40 ρ ml /(kg·m −3 ) 100
4 d 2 /mm 140 c b /(m·s −1 ) 5064
n p
E
x/m 1 d p/mm 38 c e/(m·s −1 ) [1/(s ρ p)] 1/2
33
R m/Ω 2 d x/mm 16 c f /(m·s −1 ) 5037
r/Ω 4 c ml /(m·s −1 ) 750 c 0 /(m·s −1 ) 340
2
s /(m ·N −1 ) 15.5 × 10 −12 e 33 /(C·m −2 ) 15.1 l ml /mm 20
E
33
S
α 0 /(N·m −2 ) 1.5 × 10 13 γ 0 /(N·m −1 ·V −1 ) 5 × 10 4 ε /(F·m −1 ) 562 × 10 −11
33
2
λ/(N·s m −1 kg −1 ) 8 × 10 3 β/(N·V −2 ) 6 × 10 −5 l 2p /mm 2