Page 101 - 《应用声学》2024年第1期

第 43 卷 第 1 期 陈键等： 基于低频吸声超构材料的复合消声器 97

阵列，相邻两个小孔间具有一定的间隔。穿孔管消 多种优化，尤其是针对低频段，如内嵌式、颈部旁
声器具有第一声阻抗，其函数为Z m (σ, t, d)，其中，σ 支管、多阶等 [10−13] 。为减小结构厚度，引入内嵌式
表示管道的孔隙率，t 为管道壁的厚度，d 为小孔的 HR [10] 。由于共振特性，单个 HR 吸声带宽较窄。为
孔径。传统的穿孔管消声器的消声原理在于阻抗失 拓宽吸声频带，采用共振腔阵列，通过增加腔的数
配。声波通过穿孔管的通孔时会产生阻抗效应，衰 量来增加耦合效应，即更密集的模式密度 [14] ，可等
减声波，中高频消声性能较好 [8] 。需要说明的是：穿 效为多个 HR 并联，单个 HR 各部分串联。故需要
孔管消声器的穿孔并非直接暴露在外部空气环境 对 HR 的数量、孔径、厚度及排布方式等进行优化
中，文章所展示的复合消声器管道剖面及穿孔管消 设计。
声器剖面均为所设计复合消声器核心结构，在整个 当 HR 单元中心间距较大时，将每个 HR 看作
结构外侧包裹有外壳。 局域共振。优化设计时，可以忽略单元间耦合。将
穿孔管小孔声阻抗公式如式(1) [9] 所示： HR 单元的结构参数看作离散变量，把选定频段内
√ ( )
32ηt x 2 1 最优的平均吸声系数作为 HR 结构优化模型的目
Z 0 = 1+ +jωρ 1+√ , (1)
d 2 32 9 + x /2 标函数，可分析得出优化机制。进而利用遗传算
2
其中，Z 0 为小孔声阻抗，η 为黏滞系数，t为管道壁的 法，对结构参数进行迭代寻优，以进行优化与设
厚度，d为小孔孔径，ρ为空气密度，x为频率函数。 计。接着对腔的数量、结构厚度也进行比较，最
在本设计中，穿孔管消声器包括进风口、出风 终确定了 96 个腔、整体厚度 40 mm、尺寸大小为
口、扩张腔及穿孔管，小孔孔径 d 为 20 mm，孔隙率 200 mm×300 mm的情况，该结构如图3所示。
σ 为0.5，管道壁的厚度t为3 mm。在80 ∼ 13000 Hz HR阻抗可用公式(2) [10] 表示：
(
范围内对其消声性能进行仿真，结果如图 2 所示。 A 2j sin (k ca l a /2)
Z = − ρ 0 c 0 √
可发现，在 1000 Hz 以下的频段，平均传递损失 S a (γ− (γ−1) ψ ha )ψ va
(Transimission loss, TL) 不到 4 dB，低频段消声性 jS a r cc c 2 cc √ )
− + 2 2ωρ 0 η + jωρ 0 δ i , (2)
能较差。 ωV
其中，A 为整个 HR 共鸣腔的面积；S a 为孔的面积；
100
ቈߘኮ๗ܦ٨
ρ cc 、c cc 和k cc 指的是腔中的声传播；k ca 、ψ ha 和ψ va
HR᫼ѵ
80 指的是孔中的声传播；δ i 为波辐射引起的声质量的
末端校正。
͜᤬૯ܿ/dB 40
60

20

0
100 1000 10000
ᮠဋ/Hz
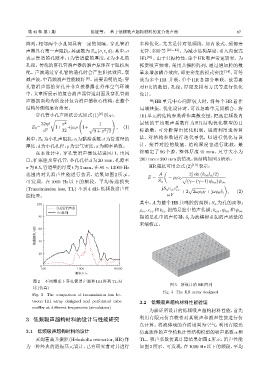
图 2 不同频率下穿孔管消声器和 HR 阵列 TL 对
图 3 所设计的 HR 阵列
比 (仿真)
Fig. 3 The HR array designed
Fig. 2 The comparison of transmission loss be-
tween HR array designed and perforated tube 3.2 低频吸声超构材料性能验证
muffler at different frequencies (simulation)
为验证所设计的低频吸声超构材料性能，首先
3 低频吸声超构材料的设计与性能研究 利用有限元仿真软件对其吸声和消声性能进行仿
真计算。将流体域的介质设置为空气，利用有限元
3.1 低频吸声超构材料的设计 仿真软件的声学模块计算结构模型的吸声系数α 和
亥姆霍兹共振腔(Helmholtz resonator, HR)作 TL。吸声系数仿真计算结果如图 4 所示，消声性能
为一种经典的谐振基元设计，已有研究者对其进行 如图 2 所示。可发现，在 1000 Hz 以下的频段，平均