Page 71 - 《应用声学》2024年第1期

第 43 卷 第 1 期 张驰等： 多通路空间声的前方四扬声器局域 Ambisonics 信号馈给法 67

将式 (1)、式 (2) 给出的扬声器方向和式 (5) 代 这时4个扬声器信号的功率之和等于单位值：
4
入式(9)后，得到4个扬声器的信号振幅所满足的线 ∑
2
A = 1. (15)
性(矩阵)方程： i
i=1
   
1 式 (13) 和式 (14) 分别是四扬声器重放时采用
A 1
   
    恒定振幅归一化和恒定功率归一化的一阶局域
 A 2   cos θ S cos ϕ S 
Y ∗   =   , (10)
    Ambisonics信号馈给法。
 A 3   sin θ S cos ϕ S 
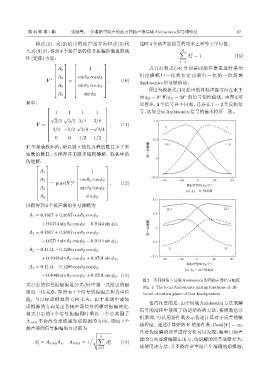
图2为根据式(13)给出的目标声源方向在水平
   
A 4 sin ϕ S
面ϕ S = 0 和ϕ S = 30 的信号馈给曲线。由图 2 可
◦
◦
其中， 以看出，4 个信号并不同相，总存在 1 ∼ 2 个反相信
 
1 1 1 1 号，这与全局Ambisonics信号的基本特征一致。
 
 √ √ 
3/2 3/2 3/4 1.0
 3/4 
Y =  √ √  , (11)
  R L
 1/2 −1/2 3/4 − 3/4 
 
0 0 1/2 1/2
0.5
Y 不是满秩矩阵，所以独立线性方程的数目少于未 RU LU
知数的数目，方程存在无限多组精确解。取其中的 ॆʷӑ૝ࣨ
伪逆解： 0
   
A 1 1
   
    -0.5
 A 2   cos θ S cos ϕ S  -90 -45 0 45 90
  = pinv(Y ) ∗   , (12)
    ᄬಖவͯᝈ θ S /(°)
 A 3   sin θ S cos ϕ S 
    (a) φ S =0° ̈́ᝈ᭧
A 4 sin ϕ S
1.0
因而得到4个扬声器的信号振幅为
RU LU
0.5
A 1 = 0.1807 + 0.3687 cos θ S cos ϕ S
ॆʷӑ૝ࣨ 0
+ 0.5714 sin θ S cos ϕ S − 0.9144 sin ϕ S ,
A 2 = 0.1807 + 0.3687 cos θ S cos ϕ S
− 0.5714 sin θ S cos ϕ S − 0.9144 sin ϕ S , -0.5
L R
A 3 = 0.1114 − 0.1286 cos θ S cos ϕ S
-1.0
+ 0.4949 sin θ S cos ϕ S + 0.9701 sin ϕ S , -90 -45 0 45 90
ᄬಖவͯᝈ θ S /(°)
A 4 = 0.1114 − 0.1286 cos θ S cos ϕ S
(b) φ S =30° ̈́ᝈ᭧
− 0.4949 sin θ S cos ϕ S + 0.9701 sin ϕ S . (13)
图 2 不同仰角下局域 Ambisonics 的四扬声器信号幅度
式 (13) 的信号振幅满足公式 (9) 中第一式给出的幅
Fig. 2 The local Ambisonics mixing functions at dif-
度归一化关系，即所有 4 个信号的振幅之和为单位 ferent elevation plane of four loudspeakers
值，与目标虚拟源的方向无关。由于重放中感知
值得注意的是，由于局域Ambisonics方法求解
虚拟源的方向是由各扬声器信号的相对振幅决定，
信号的过程中使用了伪逆矩阵的方法，按照数值分
将式 (13) 的 4 个信号振幅同时乘以一个公共因子
析原理，可以用条件数表示伪逆计算对于误差的敏
A total 不会改变重放感知虚拟源的方向。因而 4 个
感程度。通过计算矩阵Y 的条件数，Cond[Y ] = ∞，
扬声器的信号振幅也可以取为
且对伪逆解的误差进行分析可以发现，随着目标声
v
u
4
/ u∑ 源的方向逐渐偏离正前方，伪逆解的误差逐渐变大。
2
′
A = A total A i , A total = 1 t A . (14)
i
i
i=1 故使用该方法，并不能在全空间产生准确的虚拟源，