Page 122 - 《应用声学》2025年第2期

382 2025 年 3 月

际结构。对比表明采用第一种等效方式的矩形腔波 表 7 空气介质前五阶轴向模态仿真结果
纹管与实际结构波纹管模态频率差异很小，因此后 Table 7 First five order axial mode simu-
文进行理论计算时，均采用第一种等效方式对实际 lation result for air
U型波纹管进行矩形等效处理。
模态阶数 仿真结果/Hz 理论计算/Hz 偏差/%
p c p c
1 493.32 496.96 0.73
l c l c 2 989.88 993.92 0.41
3 1491.6 1490.9 −0.47
4 1998.4 1987.9 −0.52
d c
d c
5 2508.1 2484.8 −0.92
波纹管等效声速仿真结果与理论分析结果对
比表明，上文提出的波纹管内声传递模型对理想气
(a) ኄʷመ኎஍வर (b) ኄ̄መ኎஍வर
体和一般可压缩流体均有较好的适用性。
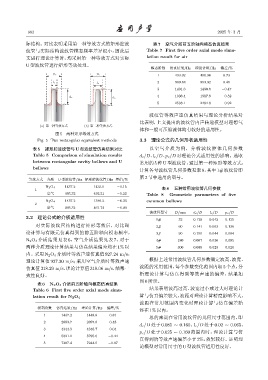
图 5 两种矩形等效方式
Fig. 5 Two rectangular equivalent methods 3.3 理论公式的几何形状适用性

表 5 矩形腔波纹管与 U 型波纹管仿真结果对比 以空气介质为例，分析波纹腔体几何参数
Table 5 Comparison of simulation results d c /D、l c /D、p c /D 对理论公式适用性的影响。选取
between rectangular cavity bellows and U 常用的 5 种 U 型波纹管，通过第一种矩形等效方式，
bellows
计算各号波纹管几何参数见表 8，其中1# 波纹管即
第2节中选用的型号。
等效方式 介质 U 型波纹管/Hz 矩形腔波纹管/Hz 差值/%
1437.2 1435.0 −0.15
N 2 O 4 表 8 五种常用波纹管几何参数
1
空气 493.32 492.21 −0.22 Table 8 Geometric parameters of five
N 2 O 4 1437.2 1346.2 −6.33 common bellows
2
空气 493.32 461.74 −6.40
波纹管型号 D/mm d c/D l c/D p c/D
3.2 理论公式的介质适用性
1# 32 0.128 0.043 0.125
对实际波纹管结构进行矩形等效后，对比理 2# 60 0.141 0.063 0.136
论计算与有限元仿真得到的前五阶轴向模态频率， 3# 90 0.150 0.044 0.084
N 2 O 4 介质结果见表 6，空气介质结果见表 7，对于 4# 180 0.087 0.036 0.085
两种介质理论计算结果与仿真结果偏差均在 1% 以 5# 300 0.088 0.023 0.026
内。采用 N 2 O 4 介质时等效声速仿真值 927.24 m/s，
理论计算值 927.30 m/s；采用空气介质时等效声速 根据上述常用波纹管几何参数确定波高、波宽、
仿真值318.29 m/s，理论计算值318.06 m/s，结果一 波距的常用范围，每个参数变化范围内取5 个点，分
致性良好。 析理论计算与仿真得到等效声速的偏差，结果如
图 6所示。
表 6 N 2 O 4 介质前五阶轴向模态仿真结果
结果表明波高过高、波宽过小或过大时理论计
Table 6 First five order axial mode simu-
算与仿真偏差较大，波距对理论计算精度影响不大，
lation result for N 2 O 4
波距在常用范围内变化时理论计算与仿真偏差始
模态阶数 仿真结果/Hz 理论计算/Hz 偏差/%
终在1%以内。
1 1437.2 1448.9 0.81
总的来说在常用波纹管的几何尺寸范围内，即
2 2883.7 2897.8 0.48
d c /D 处于 0.085 ∼ 0.160、l c /D 处于 0.02 ∼ 0.065、
3 4344.9 4346.7 0.04
p c /D 处于 0.025 ∼ 0.160 范围内时，理论计算与仿
4 5821.1 5795.6 −0.44
真得到的等效声速偏差小于2%，效果较好。证明理
5 7307.4 7244.5 −0.87
论模型对常用尺寸的U型波纹管适用性良好。