Page 141 - 《应用声学》2025年第2期

第 44 卷 第 2 期 程宇翔等： 梯度流阻率多孔材料设计与声学性能分析 401

其中材料的第一层为面向入射声波的层，对于 差，因此整体吸声系数较低；而第一层流阻率较低的
两种流阻率梯度结构，均设置了具有不同流阻率梯 材料孔径较大，通孔数量多，有利于声波进入材料而
度差的对照组，以验证结论的普适性。对于表 4 中 不是在表面被反射，并且后层较高的流阻率使得声
各种流阻率配置的材料分别计算吸声系数，结果曲 波的传播路径更加复杂，在传播过程中受到更高的
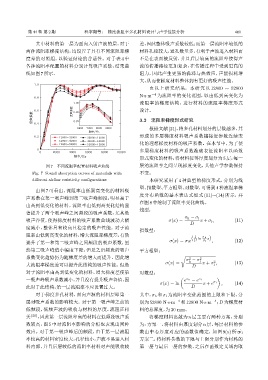
线如图7所示。 阻力，因此产生更强的黏滞与热效应，声能损耗增
大，从而使梯度材料整体拥有更好的吸声性能。
1.0
由以上研究结果，本研究以 12800 ∼ 52800
N·s·m −4 为流阻率的变化范围，以由低到高变化为
0.8
1.00 流阻率的梯度结构，进行材料的流阻率梯度形式
0.6 ծܦጇ஝ 0.96 设计。
ծܦጇ஝ 0.92 3.2 流阻率梯度形式研究

0.4
6400 7200 8000 8800 根据文献 [21]，将多孔材料划分的层数越多，其
ᮠဋ/Hz
0.2 12800~32800 32800~12800 形成的多层梯度材料吸声系数越接近参数连续变
12800~42800 42800~12800
12800~52800 52800~12800 化的理想梯度材料的吸声系数。在本节中，为了使
0 多层梯度材料的吸声系数准确表征流阻率以函数
0 2000 4000 6000 8000 10000
ᮠဋ/Hz
形式变化的材料，将材料按等厚度划分为 5层，每一
图 7 不同流阻率配置材料吸声曲线 层的流阻率之间呈现梯度变化，其他声学参数保持
Fig. 7 Sound absorption curves of materials with 不变。
different airflow resistivity configurations 本研究采用了 4 种典型的梯度形式，分别为线
型、指数型、平方根型、对数型，可得到4种流阻率梯
由图 7 可看出，流阻率由低到高变化的材料吸
度分布函数的基本表达式如式 (11)∼(14) 所示，并
声系数在第一吸声峰到第二吸声峰频段，明显高于
在图8中绘制了流阻率变化曲线。
由高到低变化的材料。流阻率由低到高变化结构显
线型：
著提升了两个吸声峰之间频段的吸声系数，尤其是
σ h − σ l
吸声谷值，使得梯度材料的吸声系数曲线波动大幅 σ(x) = x + σ l , (11)
D
度减小，整体具有较高且稳定的吸声性能。对于流
指数型：
阻率由低到高变化的材料，增大流阻率梯度差，有效 ( 1 ln σ h x )
提升了第一和第二吸声峰之间频段的吸声系数，虽 σ(x) = σ l e D σ l , (12)
然第二吸声峰值小幅度下降，但是之后频段的吸声 平方根型：

系数变化趋势仍为随梯度差的增大而提升。因此增 √ σ − σ 2
2
2
大流阻率梯度差可以提升此结构的吸声性能。但是 σ(x) = h D l x + σ , (13)
l
对于流阻率由高到低变化的材料，增大梯度差使第 对数型：
一吸声峰吸声系数减小，并且没有提升吸声谷值，因 ( e σ h − e σ l )
σ(x) = ln x + e σ l , (14)
此对于此结构，第一层流阻率不应设置过大。 D
对于梯度多孔材料，面向声源的材料层即第一 其中，σ h 和 σ l 为流阻率变化范围的上限和下限，分
层对吸声系数的影响较大。对于第一吸声峰之前的 别为 52800 N·s·m −4 和12800 N·s·m −4 ；D 为梯度材
低频段，低频声波的吸收与材料的厚度、流阻正相 料的总厚度，为30 mm。
关 [20] ，因此第一层流阻率高的材料在低频段吸声系 将梯度材料离散为 n 层主要有两种方案，分别
数较高，图 5 中对流阻率影响的分析也表现出同种 为：方案一，将材料由厚度划分 n 层，每层材料的参
效应。对于第一吸声峰后的频段，由于第一层流阻 数由中心厚度对应的函数值确定，如图 9(a) 所示；
率较高的材料密度较大，孔径较小，声波不易进入材 方案二，将材料参数的下限与上限分别作为材料的
料内部，并且后层较低的流阻率材料对声能吸收较 第一层与最后一层的参数，之后在函数定义域内取