Page 143 - 《应用声学》2025年第2期

第 44 卷 第 2 期 程宇翔等： 梯度流阻率多孔材料设计与声学性能分析 403

步提升，吸声曲线到达峰值后波动较小，提高了宽频 图 11(a) 表明，随着 a 值的减小，流阻率分布函
吸声性能。 数的曲率逐渐增大；如图 11(b) 所示，随函数的曲率
3.3 对数曲线曲率的影响 增大，材料的吸声系数在吸声谷频段均得到提升，此
结果与 3.1 节中增大流阻率梯度差能够提升材料在
为了获取更优的流阻率梯度分布，以及研究增
吸声谷处吸声系数的结论相一致。但是由图 11(b)
加梯度差对吸声系数的具体影响，在梯度函数基本
可知，吸声系数的提升幅度较小，在吸声谷频段
表达式的基础上改变曲线的曲率做进一步研究。采
5000 Hz 处最大提高约0.019。这是因为通过流阻率
用对数型作为基本梯度形式，通过改变参数来调
梯度结构与梯度形式设计，材料的后层流阻率已经
整对数函数的曲率。本研究中，对数函数的基本表
达到较高水平，在流阻率增加到一定程度后，继续增
达式为：σ(x) = a ln(bx + c)，其中 a 是影响对数函
大流阻率对材料的吸声系数提升效果有限。
数曲率的参数。经过坐标 (0, σ l )，(D, σ h ) 的所有函
( σ h /a σ l /a ) σ l /a 但是在第一吸声峰处材料的吸声系数随曲率
数 y = σ(x) 中，b = e − e /D，c = e 。
增大而有一定程度的降低，其中峰值吸声系数在
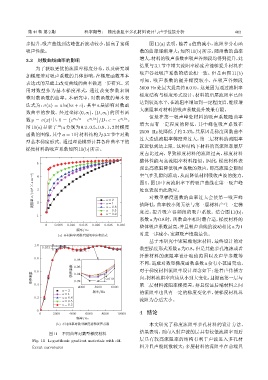
图 11(a) 显示了当 a 分别为 0.2、0.5、0.8、1、2 时梯度
2500 Hz 处降低了约 3.3%，其原因是梯度函数曲率
函数的图像，其中 a = 1 时材料结构为 3.2 节中对数
过大造成流阻率梯度差过大，第二层材料的流阻率
型基本梯度形式。通过理论模型计算各种曲率下的
就近似到达上限。这种结构下材料的高流阻率层厚
梯度材料的吸声系数如图11(b)所示。
度占比过高，导致梯度材料的流阻过高，梯度材料
整体性能与高流阻率材料相似。因此，梯度材料表
5
现出高流阻降低吸声系数的效应，即高流阻会限制
空气在孔隙间流动，从而降低材料吸收声波的能力，
ื᫾ဋ σ/(10 4 NSsSm -4 ) 3 a/ 图 5、图 10 中高流阻率下的吸声曲线在第一吸声峰
4
处也表现出此效应。
对数型梯度函数的曲率过大会使第一吸声峰
2
a/
a/⊲
a/⊲ 值降低，曲率较小则无法与第一层材料产生一定梯
度差，提升吸声谷频段的吸声系数。结合图 11(b)，
a/⊲
1
系数 a 为 0.8 时，函数曲率相对最合适，梯度材料的
0 0.005 0.010 0.015 0.020 0.025 0.030
整体吸声系数最高，并且吸声曲线的波动相比a为1
ᮠဋ/Hz
(a) ˀՏజဋࠫ஝یื᫾ဋѬ࣋ॎर 时进一步减小，宽频吸声性能最优。
基于本研究中聚氨酯泡沫材料，最终设计的对
1.0
0.033 数型梯度形式系数a为0.8。但是其他多孔泡沫或者
纤维材料的流阻率设计取值范围以及声学参数等
0.8
0.98
不同，造成对数型梯度函数系数 a 会有小范围变动。
0.96
0.6 ծܦጇ஝ 0.94 对于梯度材料流阻率设计理念如下：沿着声传播方
ծܦጇ஝ 0.92 0.019 向，材料流阻率应该从小到大变化，且提高第一层与
0.4
4000 5000 6000 第二层材料流阻率梯度差，并且保证后端材料之间
a/ ᮠဋ/Hz 的流阻率也具有一定的梯度变化率，使梯度材料总
a/
0.2 a/⊲
a/⊲ 流阻为合适大小。
a/⊲
0
0 2000 4000 6000 8000 10000 4 结论
ᮠဋ/Hz
(b) ˀՏజဋࠫ஝ی೙एెநծܦጇ஝ 本文研究了梯度流阻率多孔材料的设计方法。

图 11 不同曲率对数型梯度材料 结果表明，面向入射声波的层具有较低流阻率而后
Fig. 11 Logarithmic gradient materials with dif- 层具有较高流阻率的结构有利于声波进入多孔材
ferent curvatures 料并且声能耗散较大；多层材料的流阻率在前端具