Page 140 - 《应用声学》2025年第2期

400 2025 年 3 月

测试值相对理论值会产生微小偏差。通过对比阻抗 峰间的吸声谷，随着流阻率的增大而逐渐提升并且
管测试和理论模型计算的吸声曲线，验证了本文理 变得平缓，当流阻率为 52800 N·s·m −4 时，谷值最
论模型的准确性。 大约为 0.90。对于第二吸声峰，随着流阻率的增大，
峰值缓慢下降且频率向高频移动。当流阻率高于
3 梯度流阻率材料设计 52800 N·s·m −4 时，材料的吸声曲线在所研究频率

内随着流阻率增大表现出整体下降趋势。因此，将
3.1 流阻率变化范围与梯度结构分析
本研究中流阻率的上限取为 52800 N·s·m −4 ，下限
本文采用聚氨酯泡沫材料进行吸声系数分析，
取为原始材料的流阻率测试值12800 N·s·m −4 。
研究流阻率的梯度变化形式对于多孔材料吸声性
流阻率的梯度结构根据面向入射声波的方向
能的影响。研究所用聚氨酯泡沫的 JCA 模型参数
分为两类：流阻率由高到低变化，流阻率由低到高
如表3所示。
变化。本研究采用双层材料近似表征两类梯度变
表 3 聚氨酯泡沫参数 化结构，示意图如图 6 所示。图中材料总厚度均为
Table 3 Parameters of polyurethane foams 30 mm，双层梯度材料每层厚度均为15 mm。

流阻率/ 黏性特征 热特征 Ͱื᫾ဋెநࡏ ᰴื᫾ဋెநࡏ
材料类型 孔隙率 曲折度
(N·s·m −4 ) 长度/µm 长度/µm
聚氨酯泡沫 0.92 12800 1.12 67 850

为了确定本研究中流阻率的变化范围，需
要研究流阻率对聚氨酯泡沫材料吸声系数的影 Ͱ-ᰴื᫾ဋ೙एፇ౞ ᰴ-Ͱื᫾ဋ೙एፇ౞
响。令材料的流阻率进行线性变化，并分别取值
为 2800 N·s·m −4 、22800 N·s·m −4 、32800 N·s·m −4 、 σ/(NSsSm -4 ) σ/(NSsSm -4 )
42800 N·s·m −4 、52800 N·s·m −4 、62800 N·s·m −4 、

72800 N·s·m −4 ，其余参数不变，材料厚度均为
d/mm d/mm
30 mm。使用理论模型计算其50∼10000 Hz 频率段 Ͱ-ᰴ೙एፇ౞ื᫾ဋѬ࣋ ᰴ-Ͱ೙एፇ౞ื᫾ဋѬ࣋
内的吸声系数，结果曲线如图5所示。
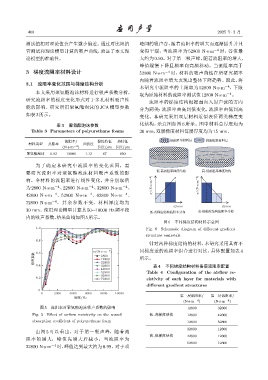
图 6 不同梯度结构材料示意图
1.0 Fig. 6 Schematic diagram of different gradient
structure materials
0.8
针对两种梯度结构的材料，本研究采用具有不
σ/(NSsSm -4 ) 同梯度差的流阻率组合进行对比，具体配置如表 4
0.6
ծܦጇ஝ 2800 所示。
12800
22800
0.4
32800
42800 表 4 不同梯度结构材料各层流阻率配置
52800 Table 4 Configuration of the airflow re-
62800
0.2 72800 sistivity of each layer for materials with
different gradient structures
0
0 2000 4000 6000 8000 10000 第一层流阻率/ 第二层流阻率/
ᮠဋ/Hz
(N·s·m −4 ) (N·s·m −4 )
图 5 流阻率对聚氨酯泡沫吸声系数的影响 12800 32800
Fig. 5 Effect of airflow resistivity on the sound 低 -高梯度结构 12800 42800
absorption coefficient of polyurethane foam 12800 52800

32800 12800
由图 5 可以看出，对于第一吸声峰，随着流
高 -低梯度结构 42800 12800
阻率的增大，峰值先增大后减小，当流阻率为
52800 12800
22800 N·s·m −4 时，峰值达到最大约为0.99。对于双