Page 189 - 《应用声学》2025年第2期

第 44 卷 第 2 期 褚润聪等： 基于向量近似消息传递均衡的超奈奎斯特水声通信 449

3.2 基于SICTE多普勒补偿结果分析 因子较大。通带接收信号功率、噪声功率和信噪比
也由表2给出，此次试验的信噪比在24∼29 dB。
对接收信号先采用 SICTE 方法估计多普勒时
为展示多普勒补偿的效果，图 9 给出了通信机
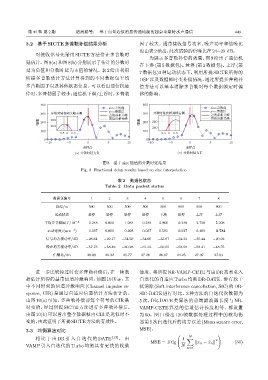
延估计。图8(a)和图8(b)分别展示了估计的分数时
在下潜 (第 5 数据包)、悬停 (第 3 数据包)、上浮 (第
延为负值和分数时延为正值的情况。表 2 给出利用
7 数据包)3 种运动状态下，利用所提 SICTE 所得的
所提多普勒估计方法计算得到的不同数据包平均 DSF 以及数据帧时变补偿情况，通过所提多普勒补
多普勒因子以及其他状态信息。可以看出通信机悬 偿方法可以基本消除多普勒对每个数据帧定时偏
停时，多普勒因子较小；通信机下潜/上浮时，多普勒 移的影响。

400 400
sincࣀϙҒ sincࣀϙҒ
ࣀϙҒ
sincࣀϙՑ sincࣀϙՑ
300 Ѭ஝௑णښᄱТ࢏ࢻΟ ࣀϙҒᄱТ࢏ 300 Ѭ஝௑णښᄱТ࢏ԿΟ ࣀϙҒᄱТ࢏
ࣀϙՑ
ࣀϙՑᄱТ࢏ ࣀϙՑᄱТ࢏
280
ࣨϙ 200 ࣨϙ 200 280
260
260
100 100
-0.5 0 0.5 -0.5 0 0.5
0 0
-10 -5 0 5 10 -10 -5 0 5 10
᧔ನག ᧔ನག
(a) Ѭ஝௑ण˞᠇ (b) Ѭ஝௑ण˞൤
图 8 基于 sinc 插值的分数时延结果
Fig. 8 Fractional delay results based on sinc interpolation

表 2 数据包状态
Table 2 Data packet status

数据包编号 1 2 3 4 5 6 7 8

深度/m 500 500 500 500 500 900 900 900
运动状态 悬停 悬停 悬停 悬停 下潜 悬停 上浮 上浮
平均多普勒因子/10 −4 −0.248 0.000 −1.984 −0.248 3.968 −0.248 −2.728 −5.208
运动速度/(m·s −1 ) −0.037 0.000 −0.298 −0.037 0.595 −0.037 −0.409 − 0.781

信号均方根功率/dB −28.64 −29.17 −34.50 −34.05 −33.67 −34.33 −30.44 −20.92
噪声均方根功率/dB −57.73 −58.49 −60.28 −61.32 −60.55 −58.58 −58.41 −48.75
信噪比/dB 29.08 29.32 25.77 27.26 26.87 24.25 27.97 27.83

进一步比较经过时变多普勒补偿后，在一帧数 速度。将所提 NR-VAMP-CETE与由 DR技术引入
据估计所得的基带信道冲激响应，如图 10 所示，其 自迭代的自适应 Turbo 均衡 DR-DATE、带有软干
中不同时刻的信道冲激响应 (Channel impulse re- 扰消除(Soft interference cancellation, SIC)的DR-
sponse, CIR) 是通过自适应信道估计方法估计的。 SIC-DATE 进行对比。3 种方法的自迭代次数都为
由图 10(a) 可知，多普勒补偿前每个符号的 CIR 是 5 次，DR-DATE 类算法的前馈滤波器长度与 NR-
时变的，经过所提 SICTE 方法进行多普勒补偿后， VAMP-CETE 算法的信道估计长度相等，都设置
由图 10(b) 可以看出整个数据帧内 CIR 是近似时不 为 60。图 11 给出 120 帧数据处理过程中的软均衡
变的，由此证明了所提SICTE方法的有效性。 器第 5 次自迭代后的均方误差 (Mean square error,

3.3 均衡算法对比 MSE)，
( N )
相 比 于 由 DR 引 入 自 迭 代 的 DATE [13] ， 由 1 ∑ 2
MSE = 10 lg ∥x n − ˆx n ∥ . (30)
VAMP 引入自迭代的 Turbo 均衡具有更快的收敛 N
n=1