Page 197 - 《应用声学》2025年第2期

第 44 卷 第 2 期 易兵等： 声学图像的水下小目标三维形状恢复 457

∑ N 方图统计特性进行自适应的获取合适的聚类个数，
足一下条件：u ij ∈ [0, 1]；∀ i, 0 < < N，
j=1
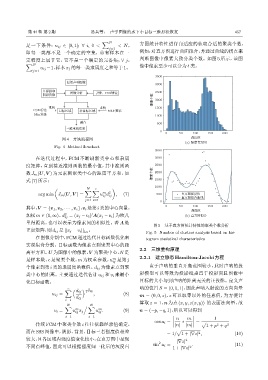
即每一类都不是一个确定的空集，总有样本在一 例如：对直方图进行曲面拟合，并通过曲线的拐点来
定程度上属于它，它不是一个确定的完备集；∀ j， 判断图像中像素大致分类个数。如图 5 所示，该图
∑ N 像中像素至少可以分为4类。
u ij =1，样本x j 的每一类隶属度之和等于1。
j=1
3500
Ԕݽܦչڏϸ
3000
ᄬಖଢԩ ڏϸѬౢ ԝ٪nj57(ܙᄞ 2500
᫻ॖ๗ᬔ
ϸጉ˔஝ 2000
᧘౞ ᧘౞ 1500
FSMካข ᄬಖӝ۫ ᭤ᄬಖӝ۫ MLFካข
Minካข 1000
ᚸՌ 500
ʼ፥᧘౞ፇ౧
0
0 50 100 150 200
图 4 方法流程图 ूएϙ
(a) ूएᄰவڏ
Fig. 4 Method flowchart
3500
在迭代过程中，FCM 不断刷新类中心和隶属 3000
度矩阵，直到接近准则函数的最小值，其中准则函 2500
数 J m (U, V ) 为元素到聚类中心的距离平方和，如 ϸጉ˔஝ 2000
式 (7)所示： 1500
1000
( N c )
∑ ∑
m 2
arg min J m (U, V ) = u d , (7) 500 ᄰவڏूएϙ
ij ij
j=1 i=1 ᄰவڏલՌజጳ
0
其中，V = {v 1 , v 2 , · · · , v c }，v i 是第i类的中心向量， 0 50 100 150 200
ूएϙ
加权m ∈ (1, ∞)。d = (x j − v i ) A(x j − v i )为欧几 (b) ᄰவڏલՌ
2
′
ij
里得距离，也可以表示为像素间的相似性。若 A 是
图 5 基于直方图统计特性的聚类个数分析
。
Fig. 5 Number of clusters analysis based on his-
正定矩阵，则d ij 是||x j − v i || L 2
在图像分割中，FCM通过迭代目标函数优化来 togram statistical characteristics
实现集合分割。目标函数为像素点到聚类中心的距
2.2 三维重构原理
离平方和。U 为图像中的像素，V 为聚类中心，N 是
2.2.1 建立静态Hamilton-Jacobi方程
m
是样本数，c 是聚类个数，m 为权重参数，u 是第 j
ij
个像素到第 i 类的隶属度函数值。d ij 为像素点到聚 由于声呐的垂直开角范围较小，此时声呐的投
类中心的距离。主要通过迭代估计 u ij 和 v i 来最小 影模型可以等效为投影线垂直于投影面且图像中
化目标函数： 目标的大小与到声呐的距离无关的正投影。定义声
呐的位置S = (0, 0, 1)，因此声呐入射波的方向向量
c ( ) 2
∑ d ij 1−m
u ij = , (8) m = (0, 0, z)，z 可以取零以外的任意值，为方便计
d lj
l=1
算取 z = 1，n 为点 (x, y, z(x, y)) 的表面法向量，故
N / N
∑ m ∑ m
v i = u x j u . (9) n = (−p, −q, 1)，所以可以得到
ij
ij
j=1 j=1
n m 1
cos a i = ∗ = √
传统 FCM 中聚类个数 c 往往依靠经验值确定， |n| |m| 1 + p + q 2
2
而在 SSS 图像中，阴影、背景、目标三者强度值相差 √ 2
= 1/ 1 + |∇z| , (10)
较大，且各区域内强度值变化较小，在直方图中呈现 |∇z| 2
2
不同点峰值，因此可以根据强度归一化后的灰度直 sin a i = 1 + |∇z| 2 . (11)