Page 201 - 《应用声学》2025年第2期

第 44 卷 第 2 期 易兵等： 声学图像的水下小目标三维形状恢复 461

从图 10的算法恢复结果可以看出，三种从明暗 同时，需要指出的是：声传播损失的影响，使得
形状恢复算法各有优缺。Min 算法对图像整体的细 靠近声呐处的目标区域回波强度大于远离声呐处
节信息恢复较好，但噪声区域容易出现毛刺现象，使 的回波强度，导致声呐图像中明亮不均匀，加上SFS
得恢复结果与实际形状存在较大差异；FSM 在一定 算法本身的缺陷造成对图像阴影区域的恢复不太
程度上保留了图像的细节信息，像素点间的关联性 理想，同时图像的信噪比对三维重构的精度有着较
相比于 Min 算法有所增强，但噪声对算法的影响依 大的影响，因此使得目标形状的恢复结果与实际物
然较大，使得三维形状起伏较大不连贯；与传统的 体形状不可避免地存在一定的差异。
FSM 和 Min 相比，本文提出的新算法 MLF 在恢复
过程中像素点与邻域像素点之间高度信息的关联 3.3 方法性能分析
性更大，较大程度上保证了目标的表面形状起伏的 本文通过在南中国海某海域利用主动声呐对
连贯性，但丢失部分细节信息。因此通过融合的方 已知目标结构的物体进行三维重构来评估方法的
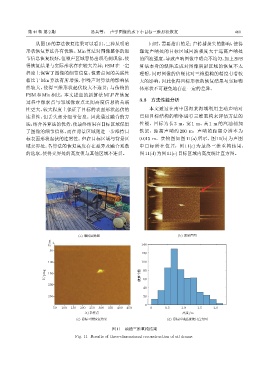
法，结合各算法的优势，使最终结果在目标区域保留 性能。目标为长 3 m、宽 1 m、高 1 m 的汽油桶加
了图像的细节信息，而在背景区域则进一步维持目 铁架，距离声呐约 200 m，声呐的距离分辨率为
标表面形状起伏的连贯性。但在目标区域与背景区 0.015 m。实物图如图 11(a) 所示，图 11(b) 为声图
域交界处，各算法的恢复高度存在差异及融合系数 中目标所在位置，图 11(c) 为最终三维重构结果，
的选取，使得交界处的高度值与其他区域不连贯。 图 11(d)为图11(c)目标区域内高度统计直方图。

(a) ෴ೋࠄྭڏ (b) Ԕݽܦڏ
Z/m 1 140

50
120
100 100

Y/ping 150 ϸጉ˔஝ 80
60
200
40

250 20
0
50 100 150 200 250 300 350 400 450 0 0.5 1.0 1.5 2.0
X⊳᧔ನག ᰴए/m
(c) ᄬಖʼ፥ূܭፇ౧ (d) ᄬಖӝ۫ᰴएፒᝠᄰவڏ
图 11 油桶三维重构结果

Fig. 11 Results of three-dimensional reconstruction of oil drums