Page 173 - 《应用声学》2025年第3期

第 44 卷 第 3 期 李健等： 利用水下滑翔机的深海影区声源深度估计 707

更大、接收距离较远时掠射角变化较慢。此外，与随 其中，R 为水平距离，α 为声线出射的掠射角，n(z)
接收距离变化不同，掠射角也随接收深度增大而变 为深度z 处的折射率，C 为积分常数。声线的传播时
化，但会根据不同声线有不同的变化趋势。由海底 间可以表示为
到达的 2 根本征声线随接收深度的增大而减小，由 φ(R, z)
t = . (3)
海面到达 2 根本征声线随接收深度的增大而增大。 c 0
各掠射角在接收深度较浅时可以认为近似相等，接 对于上述 4 条本征声线，SBR 和 BSR 声线的
收深度较深时，可以认为由海底到达的 BR 和 SBR 掠射角表示为 α SBR 和 α BSR ，2 条声线相对于 BR
的掠射角近似相等，由海面到达的 BSR 和 SBSR 的 声线存在不同的时延差，分别将其表示为 τ SBR-BR
掠射角近似相等，但不同来波方向的声线不能认为 和 τ BSR-BR ，两时延差根据公式 (4) 和公式 (5) 可以
其大小近似相等。 表达为
1
60 τ SBR-BR = (φ SBR − φ BR )
c 0
BR [
50 SBR = 1
BSR R cos α SBR − R cos α BR
c 0
SBSR
∫
40 H ( √
2
2
+ n (z) − cos α SBR
ᝈए/(°) 30 − √ n (z) − cos α BR dz
z s
)
2
2
20 ∫
H (
√
2
2
+ n (z) − cos α SBR
10 z r
)
√
2
2
− n (z) − cos α BR dz
0
5 10 15 20 25 30 ∫ z s √ ]
2
2
ᡰሏ/km + 2 n (z) − cos α SBR dz , (4)
(a) ଌஆງए300 m 0
1
70
τ BSR-BR = (φ BSR − φ BR )
BR c 0
SBR [
60 1
BSR = R cos α BSR − R cos α BR
SBSR c 0
50 ∫
H (
√ n (z) − cos α BSR
2
2
+
ᝈए/(°) 40 z s )
2
2
− √ n (z) − cos α BR dz
30
∫
H (
√
2
2
+ n (z) − cos α BSR
20
z r
)
√
2
2
− n (z) − cos α BR dz
10
0 200 400 600 800 1000 ∫ ]
z r √
ଌஆງए/m 2 2
+ 2 n (z) − cos α BSR dz . (5)
(b) ଌஆᡰሏ10 km 0
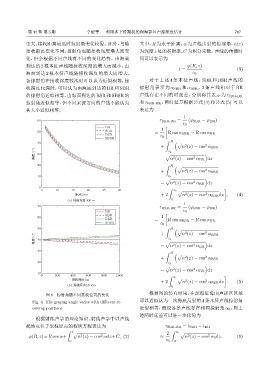
图 4 掠射角随不同接收位置的变化 根据图的仿真结果，在深海近海面声影区区域
Fig. 4 The grazing angle varies with different re- 可以近似认为一次海底反射的 4条本征声线掠射角
ceiving positions 近似相等，假设各条声线存在相同掠射角 α 0 ，则上
述两时延差可以进一步化简为
根据射线声学的理论知识，射线声学中以声线
起始点位于坐标原点的程函方程表达为 τ SBR-BR = t SBR − t BR
z
∫ ∫
√ 2 z s √
2
2
2
2
φ(R, z)=R cos α+ n (z) − cos αdz+C, (2) ≈ n (z) − cos α 0 dz. (6)
0 c 0 0